Три математических парадокса, на которых спотыкаются даже самые умные
Сушим картошку, спасаем узников и играем с бесконечностью.


Математический парадокс — это логическое противоречие, когда на первый взгляд правильные рассуждения приводят к абсурдным или взаимоисключающим выводам. Например, вот классический парадокс лжеца: если человек говорит «я сейчас лгу», это создаёт противоречие.
Если утверждение истинно, значит, человек действительно лжёт, и тогда оно становится ложным. И наоборот: если утверждение ложно, значит, человек не лжёт, что делает его истинным. То есть мы попадаем в замкнутый круг, где каждый вывод отрицает сам себя. В подобных противоречиях и заключается суть различных парадоксов.
На этом с теорией мы закончим и перейдём к разбору трёх математических парадоксов, в которые нам было трудно поверить.
Содержание
- Парадокс картофеля: как 1% воды уносит 50% массы
- Парадокс 100 заключённых: как одна хитрость превращает 0,00...1% в 31%
- Парадокс отеля Гильберта: почему ∞ + 1 = ∞, но всё же ∞ ≠ ∞
- На подумать: парадокс Монти Холла, где двери сбивают с толку
Парадокс картофеля: как 1% воды уносит 50% массы
В вашем сарае лежит 100 килограммов картофеля. Пусть 99% массы каждой картофелины — это вода. Вы оставляете картошку на ночь, и за это время она немного подсыхает. Теперь картофель состоит из 98% воды. Вопрос: сколько килограммов картофеля осталось в вашем сарае?
Казалось бы, если влажность уменьшилась всего на 1%, то и вес картошки должен сократиться на 1 кг. Но давайте немного посчитаем.
Шаг 1. Если картофель на 99% состоит из воды, то оставшийся 1% — это твёрдая часть. То есть в 100 кг будет 99 кг воды и 1 кг сухого вещества.
Шаг 2. На следующий день состав картофеля меняется: теперь в нём 98% воды, а количество сухого вещества остаётся прежним — 1 кг. Однако теперь этот 1 кг составляет уже 2% от общего веса картофеля.
Шаг 3. Решаем простую пропорцию: если 2% массы — это 1 кг сухого вещества, то 100% массы будет составлять 1 кг / 0,02 = 50 кг. То есть после высыхания наш картофель стал весить ровно в два раза меньше.

Изображение: Cmglee / Wikimedia Commons
Парадокс 100 заключённых: как одна хитрость превращает 0,00...1% в 31%
Начальник тюрьмы предлагает заключённым игру, победа в которой может принести свободу всем участникам. В тюрьме содержится 100 заключённых, и у каждого на футболке уникальный номер от 1 до 100.
Перед ними — комната с большим шкафом, в котором находится 100 пронумерованных ящиков (от 1 до 100). В каждый ящик начальник случайным образом положил листок с номером одного из заключённых.
Каждый заключённый по очереди заходит в комнату и может открыть 50 из 100 ящиков, пытаясь найти листок со своим номером. Если все 100 справятся с задачей, начальник тюрьмы отпустит их на свободу. Но если хотя бы один не найдёт свой номер, все возвращаются по своим камерам.
Заключённые не могут ничего менять в комнате, оставлять пометки или передавать информацию тем, кто ещё не заходил. Однако перед началом игры им разрешено обсудить правила и договориться о стратегии.
Вопрос: как в такой ситуации должны действовать заключённые, чтобы получить приемлемые шансы на освобождение?

Скриншот: Pygame / Skillbox Media
Перед поиском оптимального решения давайте рассмотрим самый очевидный вариант — когда все заключённые открывают 50 ящиков в случайном порядке, без какой-либо стратегии. В этом случае вероятность того, что один заключённый найдёт свой листок, составляет 1/2. Вероятность того, что два заключённых подряд найдут свои листки, равна 1/2 × 1/2 = 1/4. Для трёх подряд — 1/2 × 1/2 × 1/2 = 1/8.
Если посчитать вероятность для 100 заключённых, то получится (1/2)¹⁰⁰ ≈ 10⁻³⁰. Это невероятно маленькое число, в котором первая значащая цифра появится через нуль и ещё примерно двадцать восемь нулей после запятой. Такую вероятность можно считать почти нулевой, — видимо, именно поэтому начальник тюрьмы и согласился на игру. Но давайте попробуем увеличить шансы.

Читайте также:
Предположим, перед началом игры все заключённые договорились использовать стратегию «следуй за цепочкой». Каждый действует так:
- Сначала он открывает ящик с номером, который совпадает с его номером. Например, заключённый №25 открывает ящик №25.
- Затем смотрит, какой номер указан на бумажке внутри. Допустим, в ящике № 25 окажется спрятан номер 73.
- После этого он открывает ящик №73 и снова смотрит, какой номер внутри. Пусть это будет 14.
- Далее он открывает ящик №14 — и продолжает цепочку до тех пор, пока не найдёт свой номер или не исчерпает 50 попыток.
Эта стратегия работает благодаря тому, что все номера в ящиках распределены без повторений и пропусков — то есть образуют перестановку чисел от 1 до 100. Это значит, что каждый номер встречается ровно один раз, но не обязательно в «своём» ящике.
Такую перестановку удобно представить как набор замкнутых цепочек, или циклов. Цикл — это последовательность переходов по номерам: участник начинает с какого-то ящика, смотрит, какой номер внутри, открывает следующий ящик с этим номером, снова смотрит, что внутри, и так далее — пока не вернётся к начальному номеру. И если длина такого цикла для какого-либо заключённого не будет превышать 50, то он гарантированно найдёт нужный номер за отведённое число попыток.

Скриншот: Pygame / Skillbox Media
Если все циклы окажутся короче 51 ящика, то каждый заключённый сможет найти свой номер. Именно эта особенность и даёт шанс на всей команде. Удивительно, но вероятность того, что в случайной перестановке из 100 элементов ни один цикл не будет длиннее 50, составляет примерно 31%. Это подтверждается как математическими расчётами, так и многочисленными симуляциями этой задачи.
Ещё интереснее, что, если увеличить количество заключённых до 1 000, 10 000 или даже 100 000, вероятность успеха почти не изменится и останется на уровне 31%. То есть даже при очень большом числе участников у команды сохраняются шансы на победу. Низкие, но вполне реальные.
Но мы не предлагаем слепо верить этим цифрам — лучше убедиться во всём самостоятельно. Для этого вам понадобится:
- Установить Python для вашей операционной системы и выбрать редактор кода. Мы будем использовать Visual Studio Code.
- С помощью менеджера пакетов PIP загрузить библиотеку Pygame. Команда: pip install pygame или py -m pip install pygame.
- Создать в VS Code новый файл, например, paradox_game.py, и вставить в него код, который мы спрячем ниже под спойлером.
- Открыть терминал в VS Code и запустить игру. Команда: py paradox_game.py или python paradox_game.py.
Перед вами откроется простая версия игры, в которой можно выбрать любой ящик и двигаться по цепочке в надежде найти свой номер.
Код игры «Парадокс 100 заключённых»
import pygame
import random
import sys
N_PRISONERS = 100
DEFAULT_BOXES_IN_ROW = 20
MIN_BOX_SIZE = 28
MAX_BOX_SIZE = 100
MARGIN_RATIO = 0.12
SIDE_MARGIN_RATIO = 0.14
TOP_BOTTOM_MARGIN = 80
FPS = 60
WHITE = (245, 245, 245)
BLACK = (30, 30, 30)
GREEN = (56, 200, 100)
RED = (220, 50, 50)
GRAY = (180, 180, 180)
BLUE = (72, 140, 210)
YELLOW = (245, 213, 61)
ORANGE = (255, 150, 30)
MAX_STEPS = N_PRISONERS // 2
pygame.init()
pygame.font.init()
BASE_FONT_SIZE = 18
BASE_FONT_SMALL = 14
def create_permutation(n):
arr = list(range(1, n+1))
random.shuffle(arr)
return arr
def find_path_and_result(permutation, prisoner, max_steps):
path = []
current = prisoner
found = False
found_at = -1
for i in range(max_steps):
path.append(current)
if permutation[current - 1] == prisoner:
found = True
found_at = i + 1
path.append(prisoner)
break
current = permutation[current - 1]
return path, found, found_at
def get_grid_params(window_w, window_h):
boxes_in_row = DEFAULT_BOXES_IN_ROW
num_rows = (N_PRISONERS - 1) // boxes_in_row + 1
side_margin = int(window_w * SIDE_MARGIN_RATIO)
usable_w = window_w - 2 * side_margin
margin = max(2, int(usable_w / (boxes_in_row * 9))) # динамичный отступ
box_size = int(usable_w / (boxes_in_row + (boxes_in_row-1) * MARGIN_RATIO))
box_size = max(MIN_BOX_SIZE, min(box_size, MAX_BOX_SIZE))
grid_w = boxes_in_row * box_size + (boxes_in_row-1) * margin
grid_h = num_rows * box_size + (num_rows-1) * margin
offset_x = (window_w - grid_w) // 2
offset_y = TOP_BOTTOM_MARGIN
return box_size, margin, boxes_in_row, num_rows, offset_x, offset_y
def get_box_coords(idx, box_size, margin, boxes_in_row, offset_x, offset_y):
row = (idx - 1) // boxes_in_row
col = (idx - 1) % boxes_in_row
x = offset_x + col * (box_size + margin) + box_size // 2
y = offset_y + row * (box_size + margin) + box_size // 2
return x, y
def draw_boxes(screen, box_colors, visible_path, selected_prisoner, permutation, box_size, margin, boxes_in_row, offset_x, offset_y, font_small):
for i in range(N_PRISONERS):
row = i // boxes_in_row
col = i % boxes_in_row
x = offset_x + col * (box_size + margin)
y = offset_y + row * (box_size + margin)
color = box_colors[i]
if selected_prisoner and (i+1) == selected_prisoner:
color = BLUE
if visible_path:
if (i+1) == visible_path[-1]:
color = YELLOW
elif (i+1) in visible_path:
color = ORANGE
pygame.draw.rect(screen, color, (x, y, box_size, box_size), border_radius=int(box_size*0.22))
num_text = font_small.render(str(i+1), True, BLACK)
tx = x + (box_size - num_text.get_width()) // 2
ty = y + (box_size - num_text.get_height()) // 2
screen.blit(num_text, (tx, ty))
def draw_path(screen, path, step, box_size, margin, boxes_in_row, offset_x, offset_y):
if not path or len(path) < 2:
return
draw_to = min(step, len(path)-1)
for i in range(draw_to):
x1, y1 = get_box_coords(path[i], box_size, margin, boxes_in_row, offset_x, offset_y)
x2, y2 = get_box_coords(path[i+1], box_size, margin, boxes_in_row, offset_x, offset_y)
pygame.draw.line(screen, ORANGE, (x1, y1), (x2, y2), max(2, box_size // 17))
dx, dy = x2 - x1, y2 - y1
length = max((dx**2 + dy**2) ** 0.5, 1)
ux, uy = dx / length, dy / length
tip_x = int(x2 - ux * box_size * 0.25)
tip_y = int(y2 - uy * box_size * 0.25)
pygame.draw.circle(screen, RED, (tip_x, tip_y), max(4, box_size // 10))
def prepare_ui_lines(selected_prisoner, path, permutation, step, found, found_at_step, max_steps, game_over):
lines = []
if selected_prisoner is None:
lines.append(("Кликни по ящику: выбери свой номер заключённого!", "main", BLACK))
else:
cur_step = min(step, len(path)-1)
lines.append((f"Заключённый №{selected_prisoner}", "main", BLUE))
if found and found_at_step != -1 and cur_step >= found_at_step:
lines.append((f"УРА! Найдено за {found_at_step} шагов!", "main", GREEN))
elif game_over:
lines.append(("Игра окончена: не найдено за 50 шагов!", "main", RED))
if path and cur_step < len(path):
last_box = path[cur_step]
found_number = permutation[last_box - 1]
lines.append((f"В ящике №{last_box} спрятан номер {found_number}", "small", BLACK))
lines.append((f"Шаг: {cur_step+1} из {MAX_STEPS}", "small", BLACK))
lines.append(("ENTER -- следующий шаг | SPACE -- новая игра", "small", BLACK))
return lines
def draw_ui(screen, lines, font, font_small):
window_w, window_h = screen.get_size()
line_step = int(font.get_height() * 1.18)
total_height = len(lines) * line_step
y0 = window_h - total_height - 12
for i, (text, ftype, color) in enumerate(lines):
f = font if ftype == "main" else font_small
t_surf = f.render(text, True, color)
screen.blit(t_surf, (30, y0 + i * line_step))
def main():
WINDOW_START_W = 1320
WINDOW_START_H = 750
screen = pygame.display.set_mode((WINDOW_START_W, WINDOW_START_H), pygame.RESIZABLE)
pygame.display.set_caption("Парадокс 100 заключённых")
clock = pygame.time.Clock()
permutation = create_permutation(N_PRISONERS)
box_colors = [WHITE for _ in range(N_PRISONERS)]
selected_prisoner = None
path = []
step = 0
found = None
found_at_step = None
game_over = False
running = True
while running:
window_w, window_h = screen.get_size()
box_size, margin, boxes_in_row, num_rows, offset_x, offset_y = get_grid_params(window_w, window_h)
font_size = max(16, int(BASE_FONT_SIZE * (box_size / 35)))
font_small_size = max(11, int(BASE_FONT_SMALL * (box_size / 35)))
font = pygame.font.SysFont("consolas", font_size)
font_small = pygame.font.SysFont("consolas", font_small_size)
lines = prepare_ui_lines(selected_prisoner, path, permutation, step, found, found_at_step, MAX_STEPS, game_over)
screen.fill(GRAY)
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
elif event.type == pygame.VIDEORESIZE:
screen = pygame.display.set_mode(event.size, pygame.RESIZABLE)
elif event.type == pygame.MOUSEBUTTONDOWN:
if not game_over:
mx, my = pygame.mouse.get_pos()
for i in range(N_PRISONERS):
row = i // boxes_in_row
col = i % boxes_in_row
x = offset_x + col * (box_size + margin)
y = offset_y + row * (box_size + margin)
if x <= mx <= x+box_size and y <= my <= y+box_size:
selected_prisoner = i + 1
path, found, found_at_step = find_path_and_result(permutation, selected_prisoner, MAX_STEPS)
step = 0
game_over = False
break
elif event.type == pygame.KEYDOWN:
if event.key == pygame.K_SPACE:
permutation = create_permutation(N_PRISONERS)
box_colors = [WHITE for _ in range(N_PRISONERS)]
selected_prisoner = None
path = []
found = None
found_at_step = None
step = 0
game_over = False
elif event.key == pygame.K_RETURN:
if selected_prisoner is not None and path and not game_over:
max_show = len(path)-1
if found and step < found_at_step:
step += 1
elif not found and step < MAX_STEPS-1:
step += 1
elif not found and step >= MAX_STEPS-1:
game_over = True
cur_step = min(step, len(path)-1) if path else 0
visible_path = path[:cur_step+1] if path else []
draw_boxes(screen, box_colors, visible_path, selected_prisoner, permutation,
box_size, margin, boxes_in_row, offset_x, offset_y, font_small)
draw_path(screen, path, step, box_size, margin, boxes_in_row, offset_x, offset_y)
draw_ui(screen, lines, font, font_small)
pygame.display.flip()
clock.tick(FPS)
pygame.quit()
sys.exit()
if __name__ == "__main__":
main()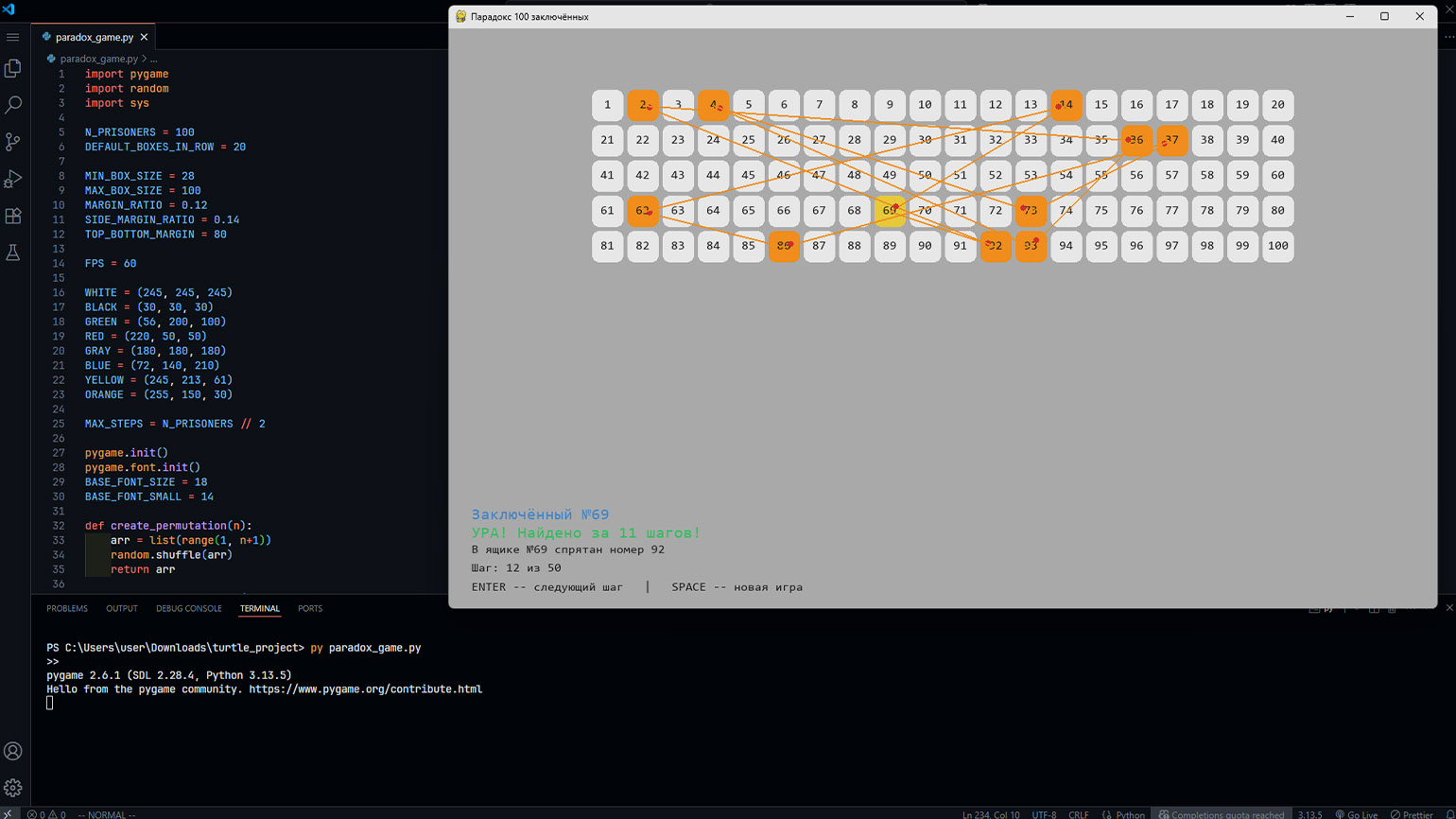
Скриншот: Pygame / Skillbox Media
Парадокс отеля Гильберта: почему ∞ + 1 = ∞, но всё же ∞ ≠ ∞
Парадокс Гранд-отеля — это мысленный эксперимент, который предложил математик Дэвид Гильберт для иллюстрации необычных свойств бесконечности. Представьте отель с бесконечным числом комнат, в котором нет свободных мест: каждая комната занята, и в каждой живёт по одному постояльцу. Давайте поэкспериментируем с этим отелем и увидим, насколько странными могут быть его свойства.
Случай первый: приходит один новый гость. На первый взгляд кажется, что разместить его невозможно, ведь отель уже полностью занят: в каждой из бесконечных комнат живёт по одному постояльцу.
Однако если попросить каждого гостя перейти на одну комнату вперёд, то первая комната освободится и в неё можно будет поселить нового гостя.
Получается парадокс: отель полностью заполнен, но для одного нового постояльца место всё равно находится. Это показывает, что у бесконечности нет предела и для неё справедливо равенство ∞ + 1 = ∞.

Читайте также:
Случай второй: приходит бесконечное число новых гостей. Просим всех постояльцев нашего переполненного отеля переехать из своей комнаты с номером n в комнату с номером 2n. Например, из комнаты 1 — в комнату 2, из 2 — в 4, из 3 — в 6, из 4 — в 8, из 5 — в 10 и так далее.
После такой перестановки все чётные комнаты окажутся заняты, а нечётные — свободны. Поскольку и тех и других бесконечно много, то в освобождённые нечётные комнаты можно заселить всех прибывших гостей. Так мы разместили одну бесконечность внутри другой: ∞ + ∞ = ∞.
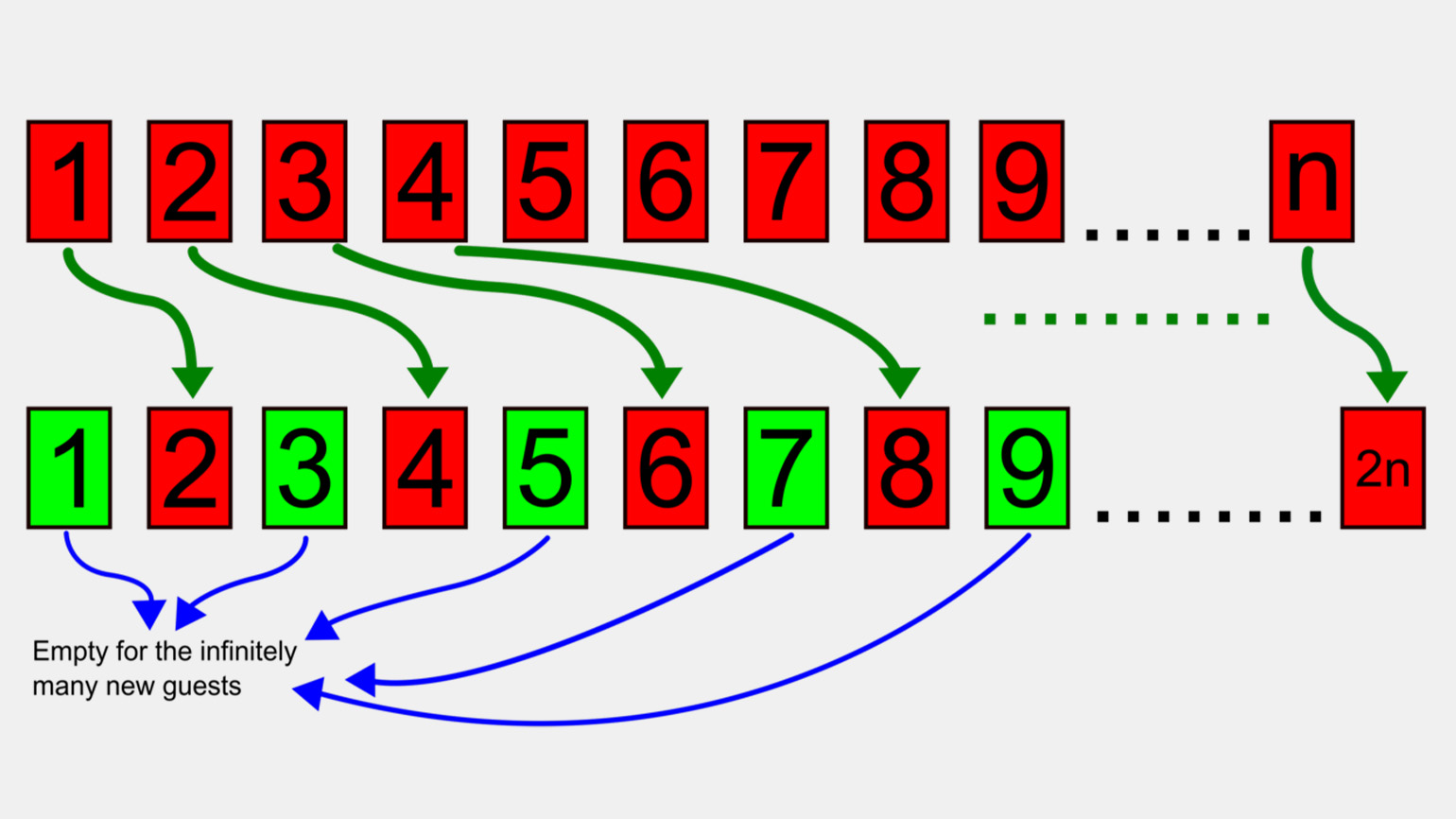
Изображение: Jan Beránek / Wikimedia Commons
Случай третий: к отелю подъезжает бесконечное число автобусов с бесконечным числом гостей в каждом. То есть в заполненном отеле нужно разместить бесконечно много бесконечностей.
Чтобы выйти из ситуации, мы можем присвоить каждому гостю уникальный номер. Для этого есть разные способы, и один из них — использование разложения чисел на простые множители. Например, если гость едет в автобусе №i и занимает место №j, то его номер комнаты можно определить по формуле: 2i × 3j. Вот как это вычисляется:
- Гость из автобуса №1, место №1: 2¹ × 3¹ = 6.
- Гость из автобуса №2, место №3: 2² × 3³ = 4 × 27 = 108.
- Гость из автобуса №3, место №2: 2³ × 3² = 8 × 9 = 72.
Также нам придётся переселить всех нынешних жильцов. Для удобства можно считать, что они приехали в автобусе №0, и расселить их по номерам по той же формуле: 2⁰ × 3ʲ = 3ʲ. Например, постояльцу из комнаты №3 придётся переселиться в комнату №27: 2⁰ × 3³ = 1 × 27 = 27.
Получается, мы нашли способ присвоить каждому постояльцу и каждому гостю своё уникальное место. То есть даже «бесконечность в квадрате» может уместиться в бесконечном отеле, если речь идёт о счётной бесконечности — о множестве натуральных чисел: ∞ × ∞ = ∞.
Случай четвёртый: мест для гостей не хватает. Представьте, что к отелю снова подъезжает бесконечное число автобусов и в каждом — бесконечное число гостей. Но теперь у каждого гостя в автобусе уже есть свой уникальный номер — не натуральное число, а любое вещественное число между 0 и 1. То есть это числа, которые можно записать как бесконечные десятичные дроби: 0,333..., 0,5, 0,14159... и так далее.
Поэтому, как бы мы ни нумеровали комнаты, расселить всех гостей не получится: вещественных чисел всегда больше, чем натуральных. Эту особенность впервые сформулировал математик Георг Кантор в теореме о различии мощностей бесконечных множеств. И это ещё один парадокс: не все бесконечности одинаковы — некоторые из них «больше» других.
На подумать: парадокс Монти Холла, где двери сбивают с толку
Представьте телевикторину с тремя дверями. За одной скрывается роскошный автомобиль, за двумя другими — симпатичные козы.
Вы выбираете, скажем, дверь №1. Прежде чем вы успеете её открыть, ведущий открывает одну из двух оставшихся дверей, за которой точно находится коза, — например, дверь №3. Затем он предлагает вам изменить выбор и выбрать дверь №2. Подумайте, стоит ли соглашаться?
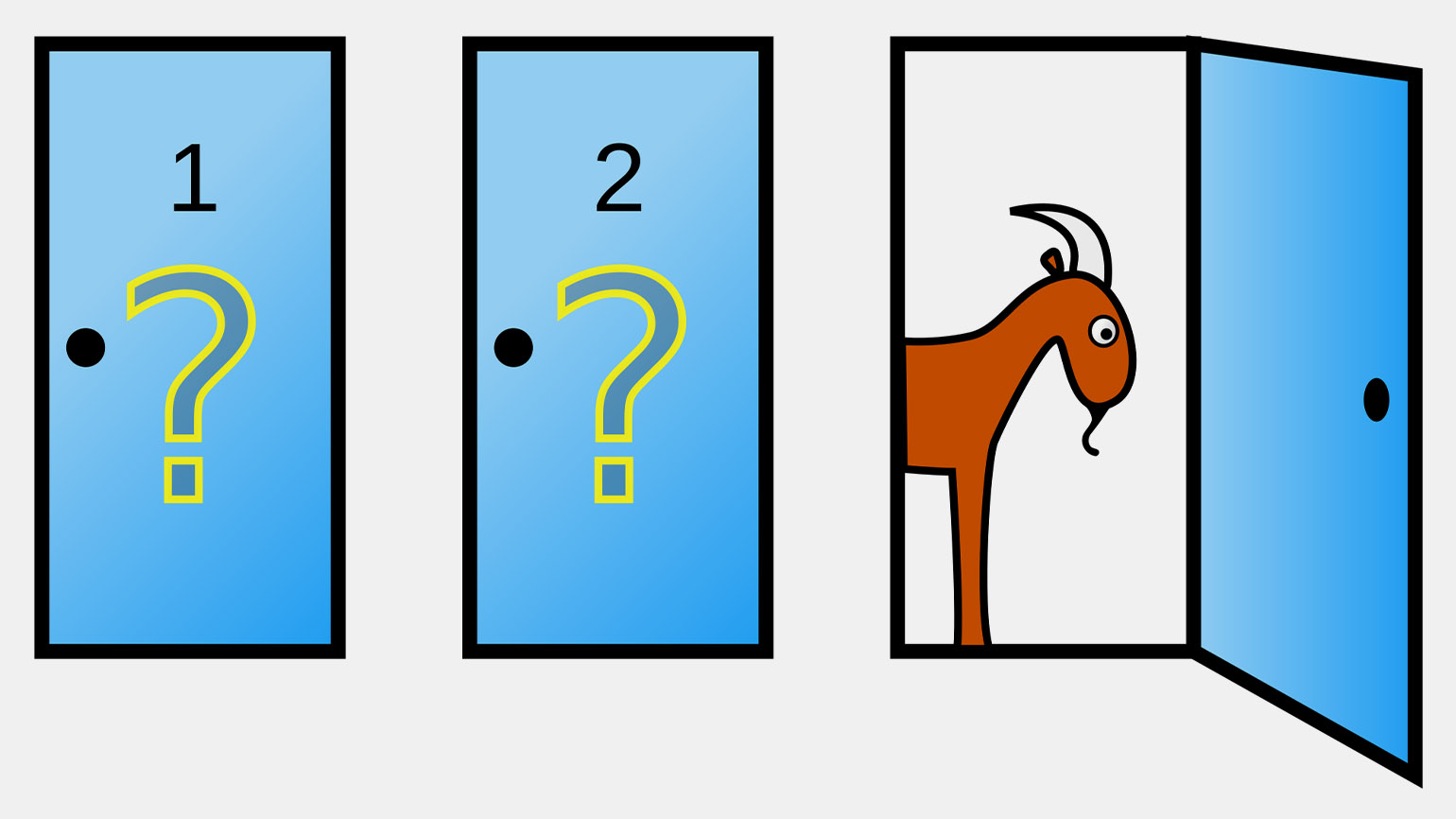
Изображение: Cepheus / Wikimedia Commons
Если вы не уверены в решении — переходите к другой статье, где мы подробно разбираем этот парадокс, предлагаем интерактивную симуляцию на Python и объясняем, почему в него так трудно поверить.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!











