Треугольник Паскаля: что это такое и в чём его магия

В математике есть простая фигура, свойства которой используют во многих областях. С её помощью решают комбинаторные задачи, вычисляют вероятности, строят фракталы и даже разрабатывают криптографические алгоритмы. В этой статье рассказываем про треугольник Паскаля — незамысловатую таблицу чисел с большим потенциалом.

Содержание

• Что такое треугольник Паскаля
• Основная формула треугольника Паскаля
• Свойства треугольника Паскаля
• Где используют треугольник Паскаля
• Примеры задач

Что такое треугольник Паскаля

Треугольник Паскаля — это математическая таблица чисел, в которой значение каждой ячейки равно сумме значений двух ячеек, стоящих над ней. Треугольник назвали в честь французского математика Блеза Паскаля, хотя свойства похожих таблиц изучали в средневековом Китае, Индии, Италии и Германии.

Треугольник Паскаля — бесконечный, а его первые десять строк выглядят так:

Треугольник строится по следующим правилам:

• В самом верху стоит единица — это нулевая строка. Нумерация строк (сверху вниз) и элементов (слева направо) начинается с нуля, а не с единицы, как мы привыкли считать.
• На рёбрах треугольника также стоят единицы.
• Каждое число, кроме единиц по бокам, равно сумме двух чисел, стоящих над ним. Например, число 3 в третьей строке равно сумме 1 и 2 из второй строки.

Всё выглядит легко, но, если внимательно изучить треугольник, можно заметить интересные свойства. Давайте рассмотрим их.

Основная формула треугольника Паскаля

Говоря формально, треугольник Паскаля — это расположение биномиальных коэффициентов для положительных целых чисел n и k. Поэтому число каждой ячейки можно найти с помощью рекуррентной формулы:

В ней:

•  — элемент в строке n и столбце k;
•  — элемент сверху слева;
•  — элемент сверху справа.

Если говорить простыми словами, то получится правило, которое мы обозначили выше: каждый элемент равен сумме чисел, стоящих над ним.

Читайте также:

Простыми словами: что такое бином Ньютона

Для примера рассмотрим вторую строку треугольника (напоминаем, что нумерация строк начинается с нуля):

Применим рекуррентную формулу, о которой говорили выше, чтобы найти число 2:

Формулу нахождения биномиальных коэффициентов можно записать в аналитическом виде:

Это уже не что иное, как формула сочетаний без повторяющихся элементов из комбинаторики. Она показывает, что элемент k-го столбца n-й строки треугольника Паскаля равен количеству способов выбрать k объектов из n без учёта повторений. Больше узнать про комбинаторику и формулы, которые в ней используют, можно в нашей статье.

Читайте также:

Перестановки, сочетания и размещения: стартер-пак по комбинаторике для IT

Свойства треугольника Паскаля

У треугольника Паскаля есть несколько интересных математических свойств. Вот некоторые из них:

• Если провести прямую вертикальную линию по центру треугольника, то части по левую и правую сторону будут симметричны. Например, в строке 1, 4, 6, 4, 1 числа расположены зеркально относительно прямой.

• Сумма всех чисел в n-й строке равна 2ⁿ. Убедимся в этом и сложим все числа пятой строки: 1 + 5 + 10 + 10 + 5 + 1 = 32 = 2⁵.

• Помимо степени двойки, в треугольнике Паскаля можно найти и квадратные числа. Для этого надо выбрать ячейку и умножить друг на друга все числа, которые её окружают. Например, 1 × 5 × 15 × 21 × 7 × 1 = 11025 = 105².

• По диагоналям треугольника Паскаля находятся последовательности чисел. На второй диагонали расположены натуральные числа, на третьей находятся треугольные, а на четвёртой — тетраэдральные. На изображении ниже мы построили диагонали справа налево, однако если поменять направление, то последовательности чисел не исчезнут.

Читайте также:

Что такое натуральные числа и как они устроены

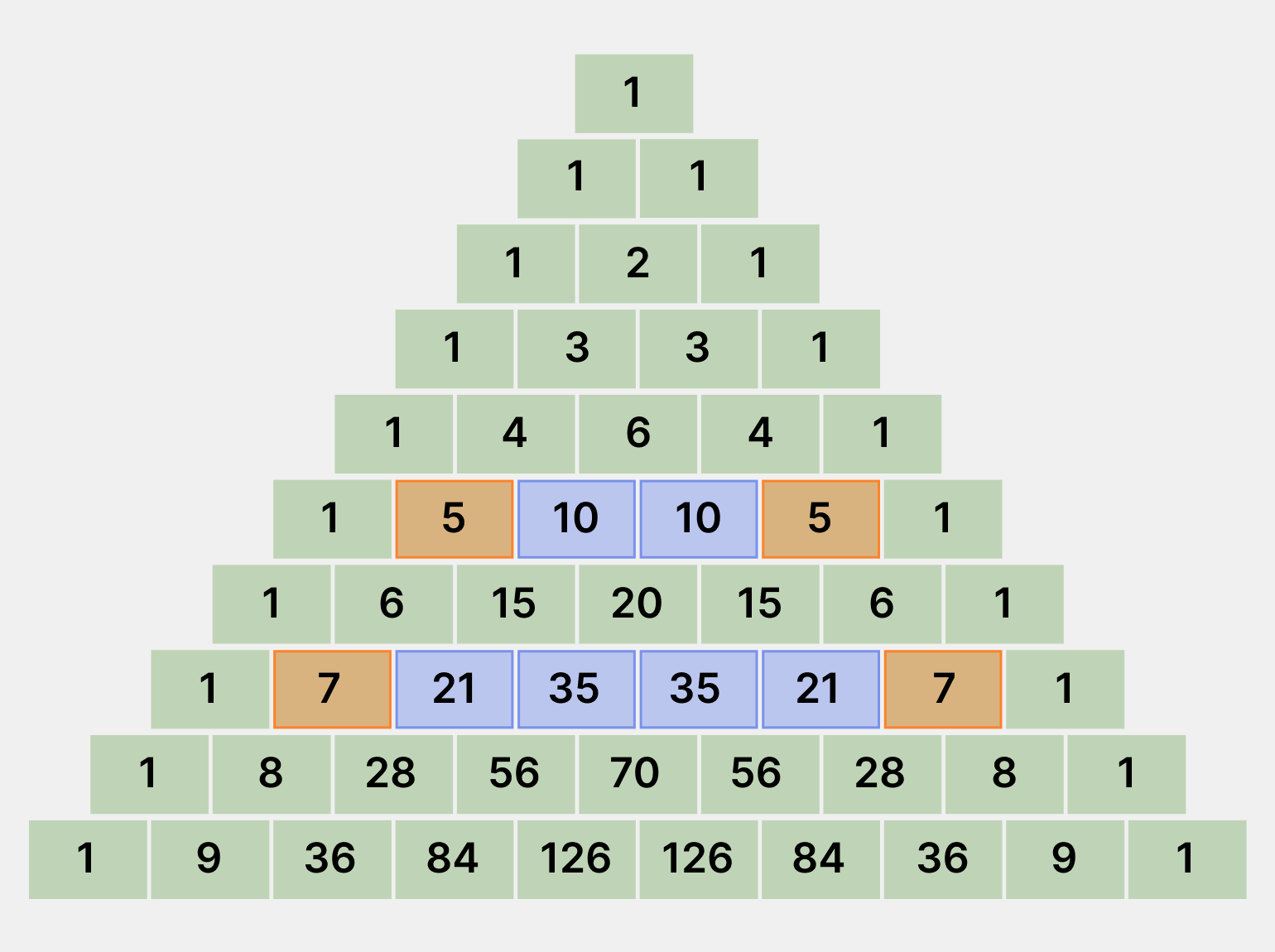
• Если второе и предпоследнее число в строке треугольника — простые, то между ними находятся числа, кратные ему. Например, в седьмой строке числа 21 и 35 делятся на простое 7, которое расположено с двух сторон от них их.

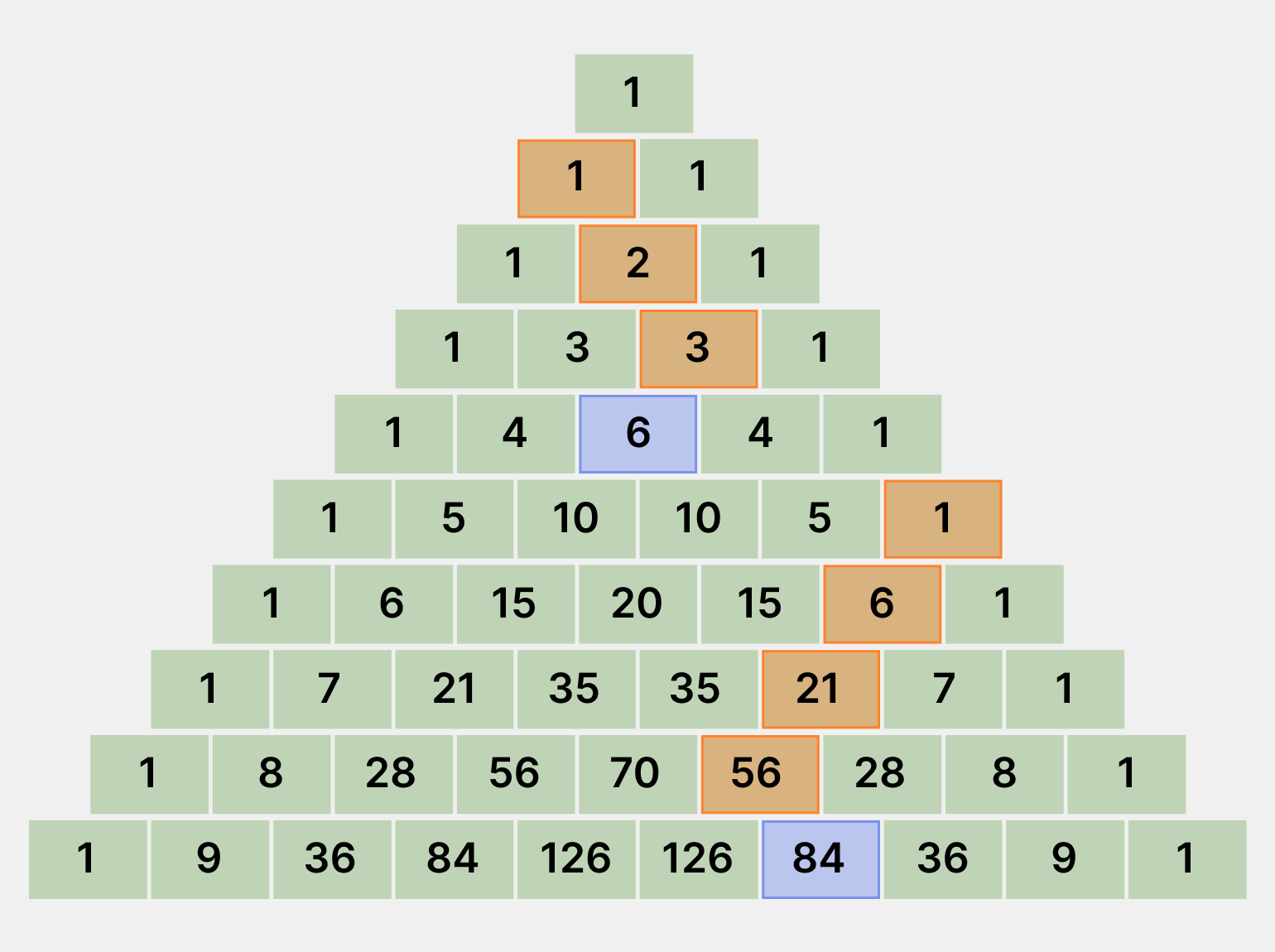
• Сумма чисел диагонали равна числу в следующей строке на противоположной диагонали. Проверим это и посчитаем сумму чисел диагонали, которая начинается в пятой строке: 1 + 6 + 21 + 56 = 84.

• Если из центрального числа строки с чётным порядковым номером вычесть соседнее число той же строки, то мы получим число Каталана.
• Число каждой ячейки треугольника Паскаля равно количеству способов попасть в эту ячейку из вершины.

Где используют треугольник Паскаля

Треугольник Паскаля тесно связан с комбинаторикой. С его помощью можно быстро и без всяких формул узнать количество способов выбрать k объектов из n без учёта повторений. Например, чтобы выяснить, сколькими способами можно взять 3 шара из 5, достаточно посмотреть на третье число в пятой строке.

Помимо комбинаторики, свойства треугольника Паскаля используют в других сферах:

• Алгебра. Выше мы уже говорили о том, что треугольник Паскаля показывает расположение биномиальных коэффициентов. Это значит, что с его помощью можно разложить бином Ньютона.
• Теория вероятностей. Треугольник Паскаля помогает решать задачи на нахождение вероятности того или иного события. Без него для нахождения промежуточных значений пришлось бы использовать формулы.

Читайте также:

Теория вероятностей: как научиться предсказывать случайные события

• Криптография. В некоторых системах шифрования применяют биномиальные коэффициенты, например в криптосистеме Пэйе.
• Фрактальная геометрия. Если построить большой треугольник Паскаля из нескольких десятков строк и закрасить все ячейки с нечётными числами, то получится треугольник Серпинского.

Практика: решаем задачи с треугольником Паскаля

Разберём задачи, для решения которых можно использовать треугольник Паскаля.

Задача 1

В кондитерском магазине есть 9 тортов разных видов. Для праздника Ивану надо купить 3 торта. Сколькими способами Иван может выбрать необходимое количество тортов?

Задача 2

Разложите выражение (a + b)⁴.

Задача 3

Какова вероятность того, что в результате пяти подбрасываний монеты два раза выпадет орёл?

Что запомнить

• Треугольник Паскаля — математическая таблица, которая показывает расположение биномиальных коэффициентов для положительных целых чисел.
• Каждое число в треугольнике равно сумме двух чисел над ним.
• Числа в строках расположены симметрично относительно центральной оси.
• Сумма чисел в каждой строке равна степени двойки номера строки.
• Свойства треугольника Паскаля используют в комбинаторике, теории вероятностей, алгебре, фрактальной геометрии и криптографии.