Основные логические (битовые) операции: что это и как они работают
Учимся умножать и складывать логически.

Логические (битовые) операции — это действия, которые программисты используют для работы с битами. Таких операций существует несколько: AND (И), OR (ИЛИ), XOR (исключающее ИЛИ), NOT (НЕ), а также побитовые сдвиги влево и вправо. Ещё существуют операторы NAND и NOR, но они не относятся к основным, поэтому в этой статье рассматривать их не будем.
Операции с логическими значениями впервые описал математик Джордж Буль — отсюда в языках программирования появилось ключевое слово boolean (bool), которое обозначает тип данных для хранения логического битового значения. Оно может быть равно 1 (истина) или 0 (ложь).
Логическая (битовая) операция XOR (исключающее ИЛИ)
Побитовый оператор XOR обозначается знаком ^. Результат этой операции истинен, когда только один из битов равняется единице. Вот так это выглядит в таблице истинности:
| A | B | A ^ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Операция XOR широко применяется в криптографии при шифровании данных. Для этого нужен специальный ключ, с помощью которого информацию можно будет закодировать.

Читайте также:
Давайте зашифруем слово hello ключом ABC. Для этого переведём каждый символ по таблице ASCII в двоичную систему счисления. У нас получится следующее:
- h = 1101000;
- e = 1100101;
- l = 1101100;
- o = 1101111;
- A = 1000001;
- B = 1000010;
- C = 1000011.
Теперь, используя оператор XOR, зашифруем каждый символ слова hello каждым последующим символом ключа. Такой алгоритм можно реализовать на любом языке программирования, мы сделали это на Java:
// Объявляем сообщение и ключ для кодирования
String message = "hello";
String key = "ABC";
// Получаем массивы символов из строк
char[] charsOfMessage = message.toCharArray();
char[] charsOfKey = key.toCharArray();
// Создаём переменную для хранения закодированного сообщения
String encryptedString = "";
for (int i = 0; i < charsOfMessage.length; i++) {
// Выводим на экран каждую операцию
System.out.println(charsOfMessage[i] + " ^ " + charsOfKey[i % key.length()] + " = " + (char) (charsOfMessage[i] ^ charsOfKey[i % key.length()]));
// Кодируем каждый символ
encryptedString += (char) (charsOfMessage[i] ^ charsOfKey[i % key.length()]);
}Если запустить код, то в терминале появятся символы ) ' / — -. Именно так и выглядит зашифрованное слово hello:
h ^ A = )
e ^ B = '
l ^ C = /
l ^ A = -
o ^ B = -
Алгоритм посимвольно кодирует слово hello каждым последующим символом ключа ABC, а под капотом компьютер переводит каждый символ в двоичную систему счисления и применяет оператор XOR:

Для расшифровки получившегося значение нужно снова провести операцию XOR со строкой) ' / — - и нашим ключом:
// Делим на символы зашифрованную строку
char[] charsOfEncString = encryptedString.toCharArray();
for (int i = 0; i < charsOfEncString.length; i++) {
// Выводим в консоль текущую операцию
System.out.println(charsOfEncString[i] + " ^ " + charsOfKey[i % key.length()] + " = " + (char) (charsOfEncString[i] ^ charsOfKey[i % key.length()]));
// Кладём в переменную расшифрованный символ
encryptedString += (char) (charsOfEncString[i] ^ charsOfKey[i % key.length()]);
}Как вы видите, мы снова получили исходное значение — hello:
) ^ A = h
' ^ B = e
/ ^ C = l
- ^ A = l
- ^ B = o
Логическая (битовая) операция AND (И)
Побитовый оператор AND обозначается символом &. AND делает то же, что и обычное умножение, поэтому в большинстве случаев в таблице истинности результат будет ложным:
| A | B | A & B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Например, совершим логическое умножение букв R и Y. Для этого с помощью таблицы ASCII найдём двоичные значения букв и столбиком перемножим каждый бит:
| R | B | A & B | ||||||
|---|---|---|---|---|---|---|---|---|
| Y | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| R | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| R & Y | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Мы получили двоичное число 01010000, которое по таблице ASCII равняется числу 80 и букве P. Логическое умножение также можно реализовать в виде кода, к примеру, на Java:
int r = 'R';
int y = 'Y';
System.out.println(Integer.toBinaryString(r));
System.out.println(Integer.toBinaryString(y));
System.out.println("_______");
System.out.println(Integer.toBinaryString(r & y));Метод Integer.toBinaryString() позволяет посмотреть, как тот или иной символ выглядит в двоичной системе счисления. Эти строки указаны лишь для примера, чтобы посмотреть, как работает операция AND. Скрипт будет правильно работать, даже если в нём будет только последняя строчка с логическим умножением:
1010010
1011001
_______
1010000

Читайте также:
Логическая (битовая) операция OR (ИЛИ)
Побитовый оператор OR обозначается знаком |. Этот оператор работает как обычное арифметическое сложение. Единственное исключение в том, что отсутствуют разряды, то есть при сложении двух единиц всё равно получится единица (1 | 1 = 1):
| A | B | A | B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Для примера напишем скрипт, который просчитает значения таблицы истинности и выведет её в консоль. В первой строчке объявим массив возможных комбинаций таблицы истинности, а далее в цикле проведём операцию OR с каждой парой значений:
int[][] bits = new int [][]{{0,0}, {0,1}, {1,0}, {1,1}};
for (int i = 0, j = 0; i < bits.length; i++)
System.out.println(bits[i][j] + " | " + bits[i][j + 1] + " = " + (bits[i][j] | bits[i][j + 1]));Если запустить код, то в консоли появится таблица истинности для операции OR:
0 | 0 = 0
0 | 1 = 1
1 | 0 = 1
1 | 1 = 1
Логическая (битовая) операция NOT (НЕ)
Побитовый оператор NOT обозначается знаком ~. NOT — унарный логический оператор, то есть применим только к одному биту. Операция инвертирует 0 в 1 и наоборот. Его ещё называют логическим отрицанием:
| A | ~A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Рассмотрим, как логическая операция NOT работает с цветами RGB-палитры. Каждый цвет в компьютере закодирован тремя числовыми значениями, которые мы можем перевести в двоичную систему счисления.
Например, чёрный цвет в RGB-палитре записывается тремя нулям: (0, 0, 0), а в двоичной системе счисления это будет (00000000, 00000000, 00000000). Если инвертировать каждое значение оператором ~ (NOT), то у нас получится (11111111, 11111111, 11111111). В десятичной системе счисления это будет (255, 255, 255), а в RGB-палитре так записывается белый цвет:

Логические операции побитовых сдвигов
Операторы побитового сдвига обозначаются двумя знаками: >> (сдвиг битов вправо) и << (сдвиг битов влево). С помощью этих операторов можно сдвинуть всю битовую цепочку влево или вправо.
| R | B | A & B | ||||||
|---|---|---|---|---|---|---|---|---|
| X | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Например, возьмём переменную X, равную 4, что в двоичном представлении будет 100:Если мы применим оператор побитового сдвига влево <<, то получим двоичное значение 1000, что в десятичном представлении будет равняться 8. Видно, что значение увеличится в два раза:
| R | B | A & B | ||||||
|---|---|---|---|---|---|---|---|---|
| X | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
Если мы применим сдвиг вправо >>, то значение уменьшится в два раза. К примеру, возьмём число 32:
| R | B | A & B | ||||||
|---|---|---|---|---|---|---|---|---|
| X | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
Операциями побитового сдвига можно заменить деление и умножение на два. В реальных проектах надо внимательно применять эти операторы, так как в языках программирования они реализованы по-разному.
В некоторых языках программирования, например Java, Kotlin, C# и JavaScript, есть оператор >>> — беззнаковый сдвиг битов вправо. Дело в том, что в двоичном представлении чисел в этих языках, если первый бит равен нулю, значит, число положительное, а если единице — отрицательное. В таком случае обычная операция сдвига не трогает самый первый бит, оставляя число с тем же знаком. А операция беззнакового сдвига перемещает все биты:

Самое главное
Сегодня вы узнали, какие существуют основные логические операции и как они работают. Кратко пройдёмся по каждому оператору:
- AND (И) — обозначается знаком & и умножает биты друг на друга. Значение истинно, когда оба бита равны единице.
- OR (ИЛИ) — обозначается знаком | и складывает два бита, не превышая разряда числа. Значение истинно, когда один или два бита равны единице.
- XOR (исключающее ИЛИ) — обозначается как |. Истина, если только один бит равен единице.
- NOT — инвертирование бита. Единицу превращает в ноль и наоборот.
- >> — побитовый сдвиг вправо. Сдвигает цепочку битов вправо. Применяясь в программировании, эта операция не изменяет положительность или отрицательность числа.
- << — побитовый сдвиг влево. Сдвигает биты влево, с конца добавляя ноль. Положительность или отрицательность также не изменяет.
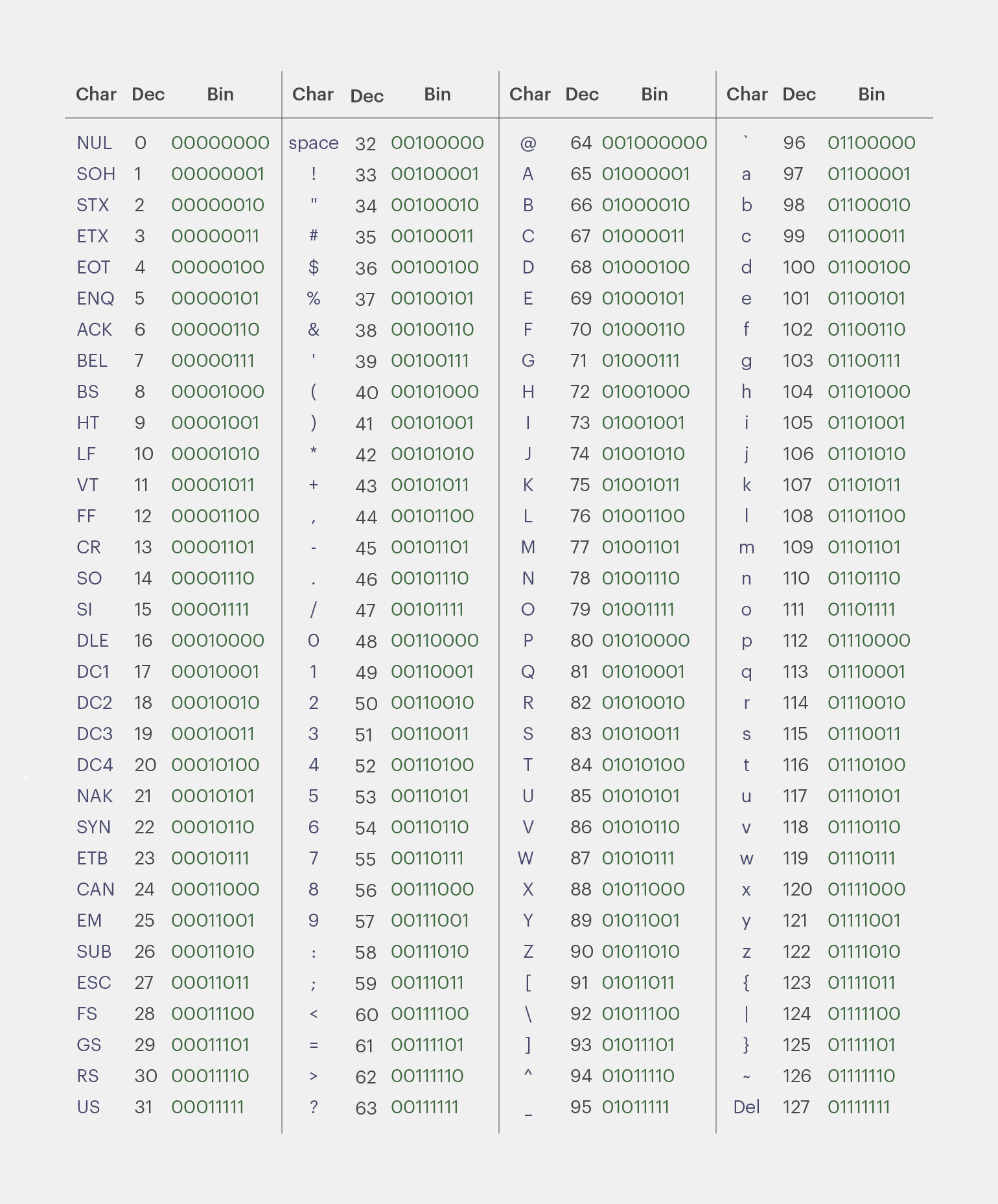
Таблица ASCII
ASCII — стандарт кодирования букв латинского алфавита, цифр, знаков препинания и специальных символов. В 1963 году Американская ассоциация стандартов приняла ASCII как основной способ представления текста в компьютере.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!




