Квадратичная функция и построение параболы: графики, формулы, свойства
Строим параболу и изучаем её свойства.

Понятие «квадратичная функция» может звучать запутанно, но на самом деле это старая добрая парабола. В этой статье рассказываем, как построить график квадратичной функции, разбираемся, в каких сферах эти знания используют, а в качестве бонуса показываем, как автоматизировать построение параболы с помощью Python.
Содержание
Что такое квадратичная функция
Функция в математике — это правило, которое сопоставляет каждому значению входной переменной одно-единственное значение выходной переменной. Например, функция может принимать на вход число (аргумент), возводить умножать его на установленный коэффициент и возвращать результат.
Функция записывается так:
y = f(x)
Её можно задать несколькими способами.
- С помощью математической формулы, например y = x2.
- С помощью таблицы с заданными парами входных и выходных значений:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 0 | 1 | 4 | 9 | 16 |
- Используя график на координатной плоскости. Каждая точка на графике соответствует паре значений (x, y), где y — это значение функции при данном x.
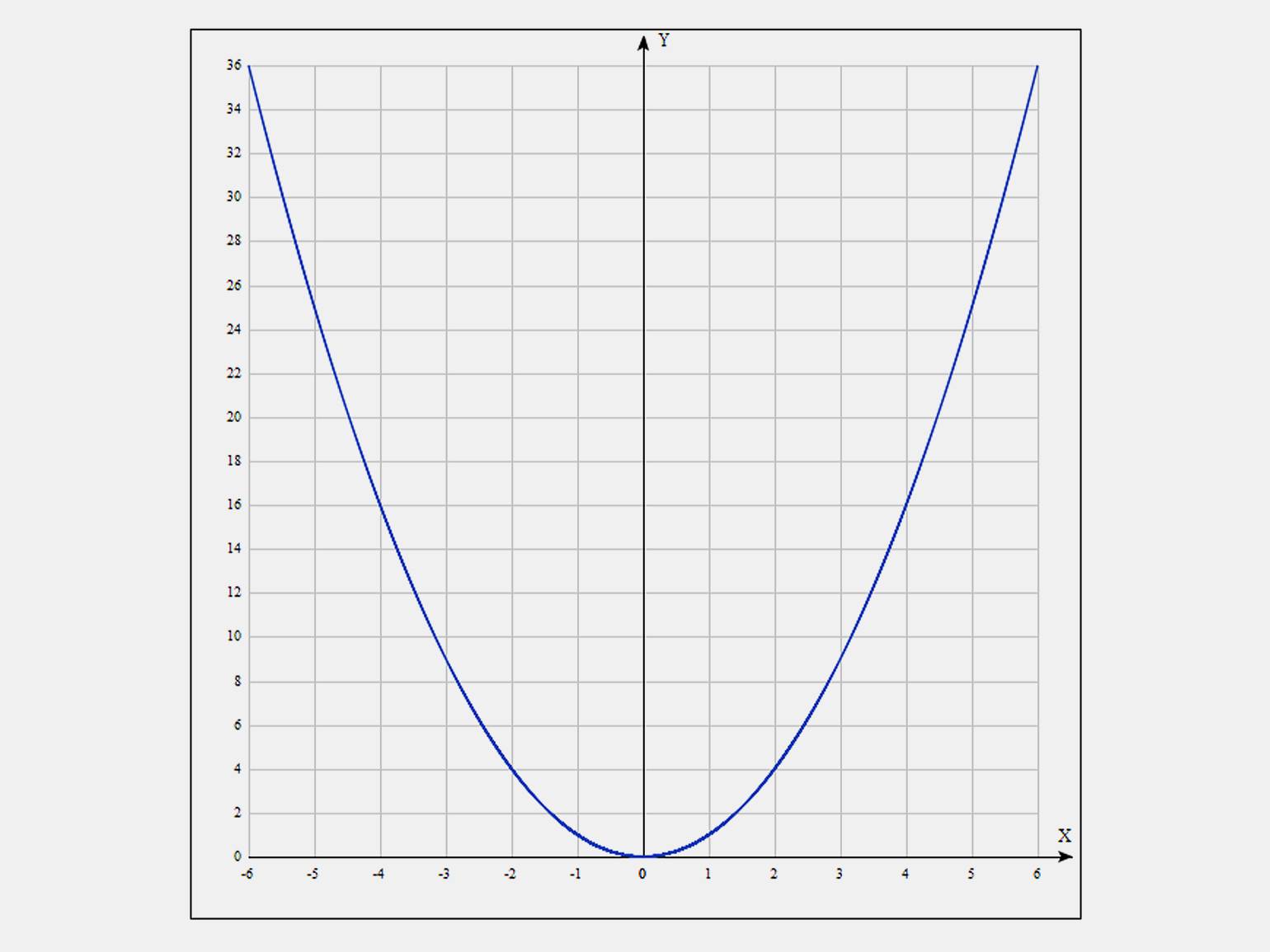
Инфографика: Skillbox Media
- С помощью словесного описания. Функцию описывают словами, объясняя, как каждое входное значение преобразуется в выходное. Например: «Возвести число в квадрат и вычесть 6» — описание функции y = x2 − 6.
Квадратичная функция — особый вид математических функций, который в виде общей формулы записывается как y = ax2 + bx + c. Где:
- x — переменная;
- a, b, c — коэффициенты.
⚠️ Важно
Коэффициенты квадратичной функции могут быть любыми числами, кроме коэффициента a, который не должен равняться нулю, иначе функция не будет квадратичной.
График квадратичной функции — парабола. Это незамкнутая симметричная кривая, имеющая две однонаправленные ветви, которые напоминают букву U. Через вершину параболы проходит вертикальная линия — ось симметрии.
Строим параболу
Форма параболы и её расположение на координатной плоскости зависят от коэффициентов квадратичной функции y = ax2 + bx + c, которая её образует.
Из чего состоит парабола
Коэффициент a (старший коэффициент). Если a > 0, то ветви параболы направлены вверх, если a < 0, то вниз. С увеличением значения a парабола становится шире, с уменьшением — уже.
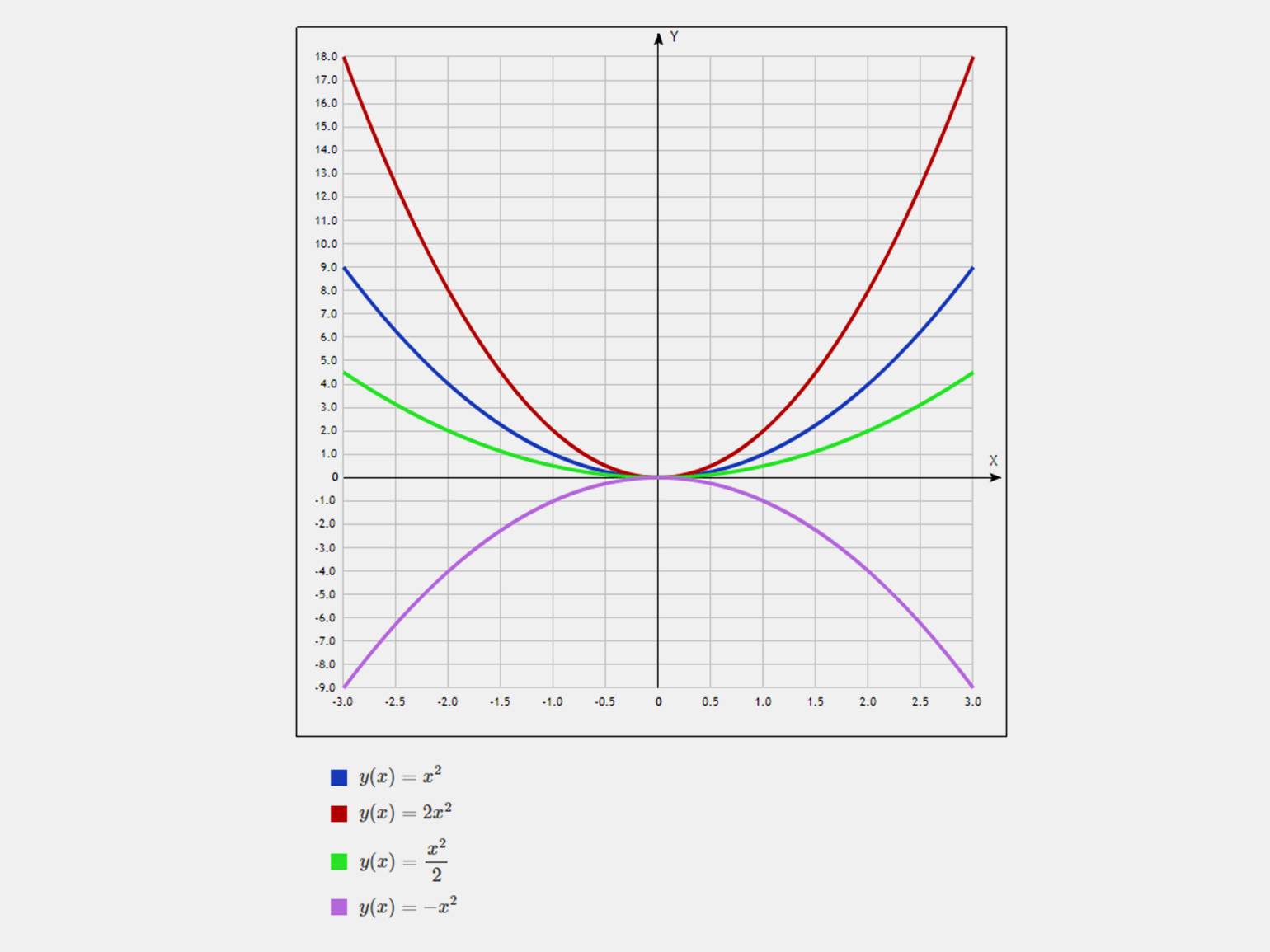
Инфографика: Skillbox Media
Коэффициент b. Определяет положение вершины параболы, которая находится в точке с координатами (−b/2a, y(−b/2a)). Если b = 0, вершина находится на оси Y, как мы видим на предыдущем рисунке. Изменение коэффициента b смещает вершину по оси X. Увеличение b сдвигает параболу вправо, а уменьшение — влево.
В примере ниже вершина параболы для функции y = x2 + 2x находится в точке (−1, −1), а для функции y = x2 − 2x — в точке (−1, 1).
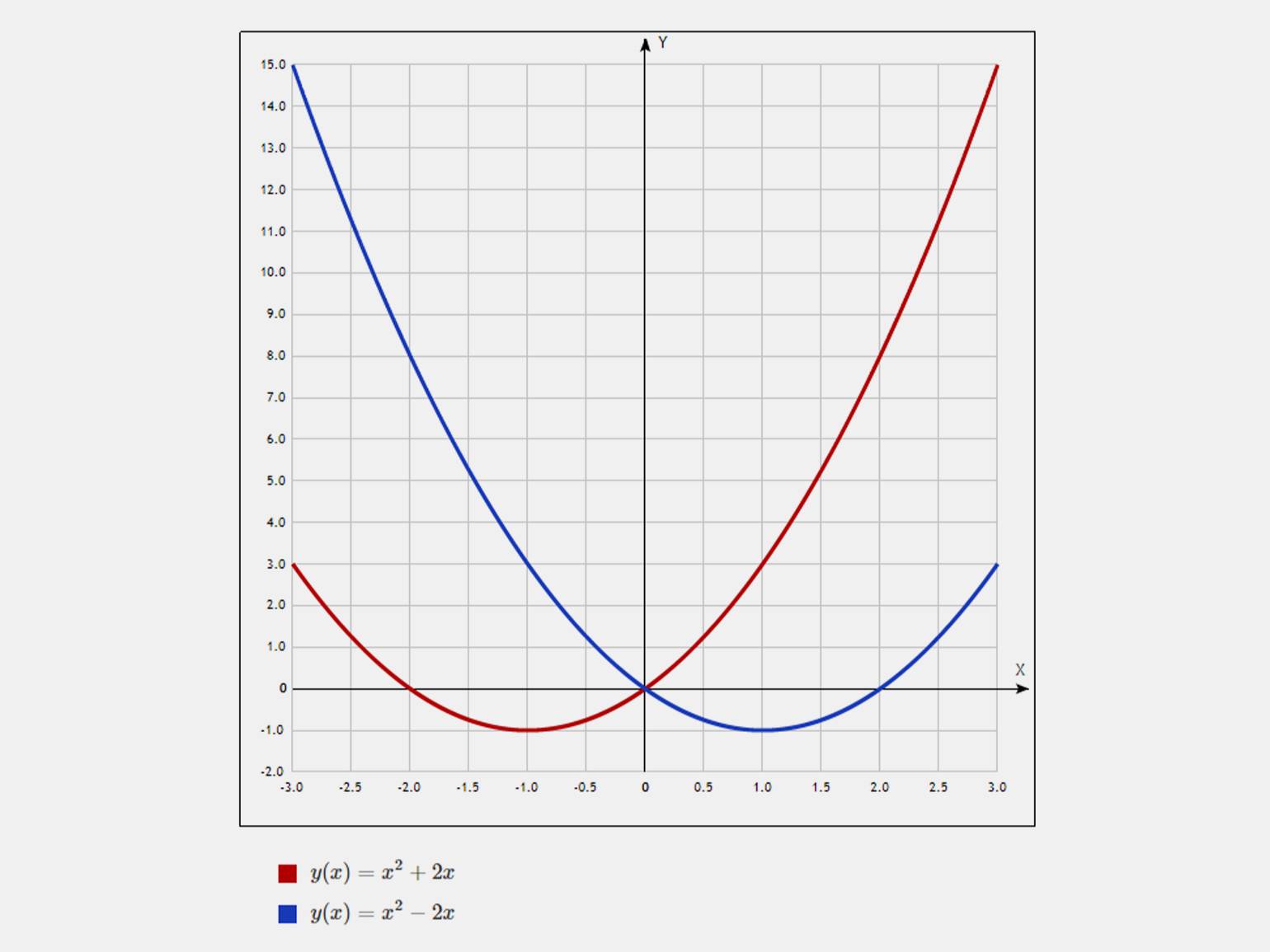
Инфографика: Skillbox Media
Коэффициент c (свободный член). Определяет точку пересечения параболы с осью Y. При изменении коэффициента c график функции перемещается вдоль вертикальной оси Y, но его форма не меняется. В примере ниже мы видим, что при уменьшении c парабола сдвигается вниз, а при увеличении — вверх.
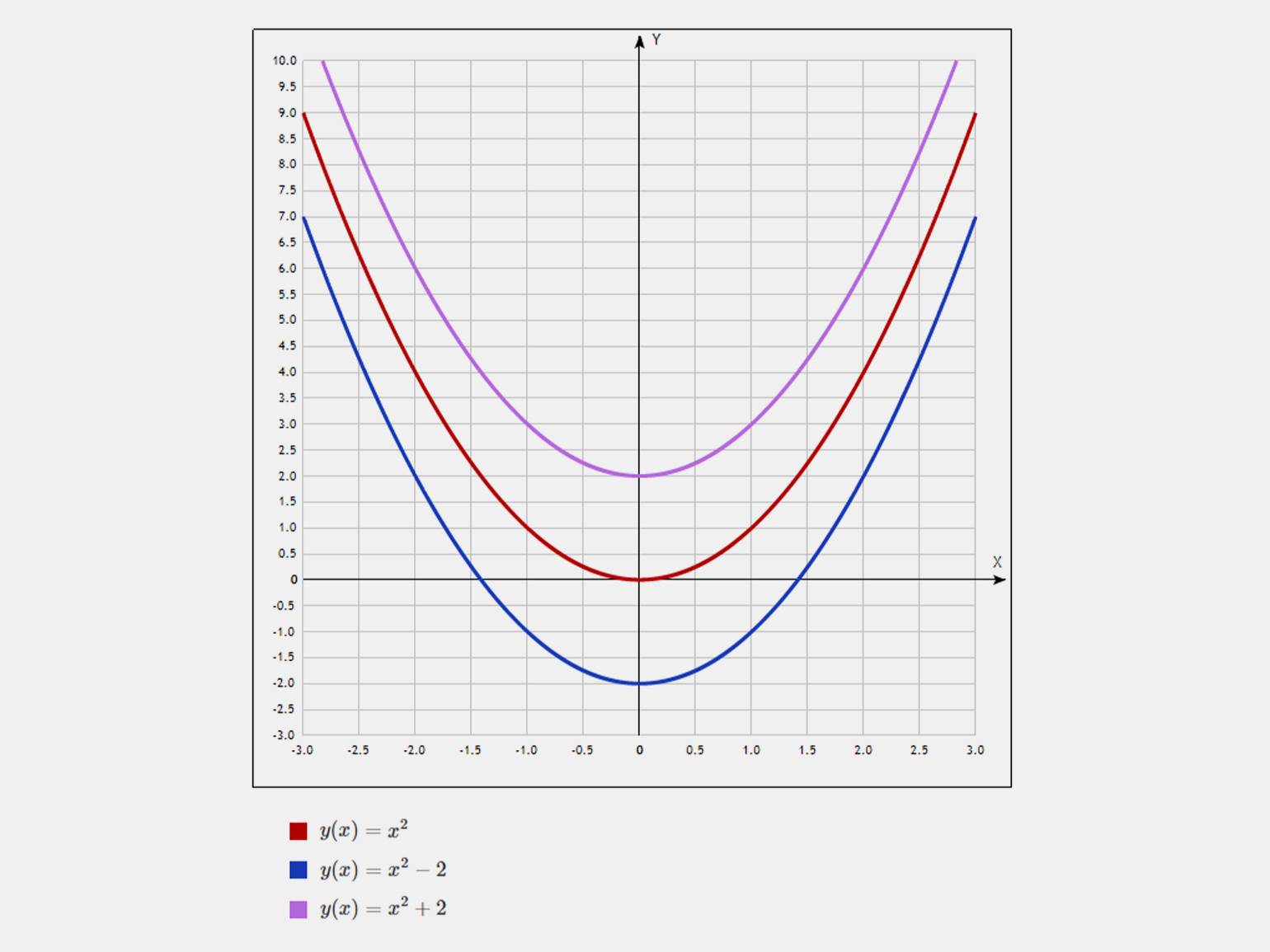
Инфографика: Skillbox Media
Как построить график квадратичной функции
Перед тем как построить параболу, надо найти точки пересечения графика функции y = ax2 + bx + c с осью X. Для этого нужно решить квадратное уравнение
ax2 + bx + c = 0.
Количество точек пересечения зависит от дискриминанта уравнения D = b2 − 4ac:
- Если D > 0, то у графика будет две точки пересечения с осью X.
- Если D = 0, вершина параболы соприкасается с осью X всего в одной точке.
- Если D < 0, то парабола не пересекается с осью X.
Чтобы построить график функции y = ax2 + bx + c, нужно:
- Определить направление параболы, которое зависит от коэффициента a.
- Найти вершину параболы — она находится в точке с координатами
x = −b / (2a) и y = c − (b2) / (4a). - Найти ось симметрии — она проходит через вершину параболы параллельно оси Y.
- Найти точки пересечения параболы с осью X.
- Найти точку пересечения с осью Y.
- Для большей точности можно добавить несколько дополнительных точек. Для этого нужно подставить несколько значений x в уравнение, чтобы найти соответствующие значения y.
Полученные точки нужно нанести на координатную плоскость и соединить между собой плавной линией.
Визуализация на Python
Проще всего построить график функции y = x2 − x − 2 c помощью Python. Это быстрее, чем искать все значения вручную. Кроме того, полученный скрипт можно будет переиспользовать.
Для нашего кода будем использовать сторонние библиотеки — NumPy и Matplotlib. Первая нужна для некоторых математических функций, а вторая — для построения графика. Можно обойтись без NumPy, но тогда придётся потратить больше времени на реализацию сложных функций.
Читайте также:
С помощью Python мы закодировали алгоритм построения параболы. Теперь в него можно просто подставить любые значения коэффициентов функции
y = ax2 + bx + c и получить визуализацию на экране компьютера:
# Импортируем библиотеки
import numpy as np
import matplotlib.pyplot as pl
# Задаём коэффициенты функции
a = 1
b = -1
c = -2
# Определяем диапазон значений x
x = np.linspace(-3, 3, 400)
y = a * x**2 + b * x + c
# Находим вершину параболы
top_x = -b / (2 * a)
top_y = a * top_x**2 + b * top_x + c
# Построение графика
pl.figure(figsize=(8, 6))
pl.plot(x, y, label='y = x^2 - x - 2', color='blue')
pl.scatter([top_x], [top_y], color='red', zorder=5)
# Вершина параболы
pl.axvline(x=top_x, color='gray', linestyle='--', label='Ось симметрии')
# Отметим точки пересечения с осями координат
y_intercept = c
# Корни уравнения для нахождения точек пересечения с осью x
x_intercepts = np.roots([a, b, c])
pl.scatter([0], [y_intercept], color='green', label='Точка пересечения с осью y', zorder=5)
pl.scatter(x_intercepts, [0, 0], color='purple', label='Точки пересечения с осью x', zorder=5)
# Настройки графика
pl.title('График квадратичной функции y = x^2 - x - 2')
pl.xlabel('x')
pl.ylabel('y')
pl.legend()
pl.grid(True)
pl.axhline(0, color='black',linewidth=0.5)
pl.axvline(0, color='black',linewidth=0.5)
pl.show()Помимо самого графика, на рисунке автоматически отмечаются точки пересечения, вершина параболы и ось симметрии:
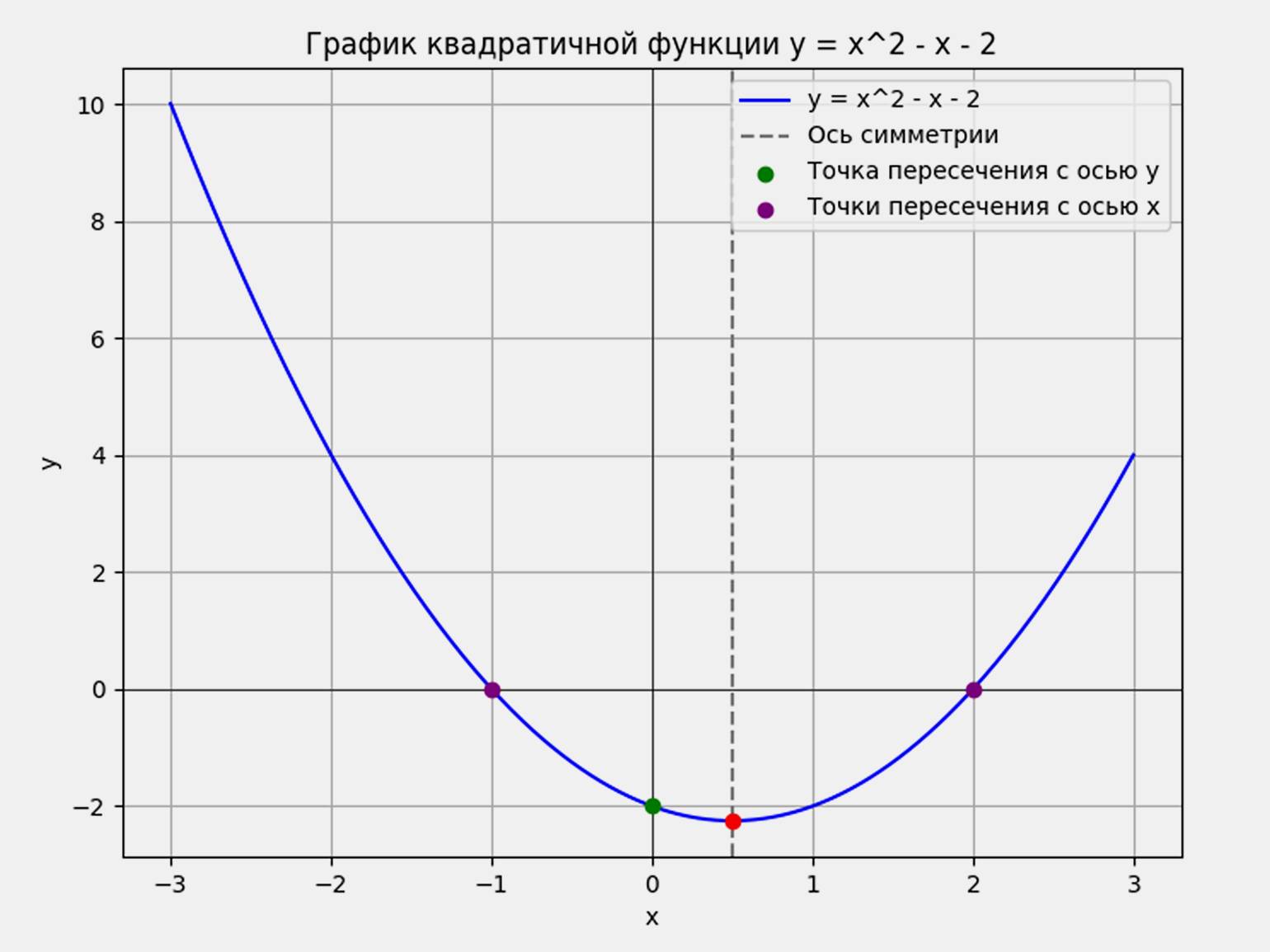
Инфографика: Skillbox Media
Читайте также:
Факты о параболе
Парабола представляет собой сечение конуса. Представьте конус с вершиной, направленной вверх. Возьмём плоскость, которая пересекает этот конус параллельно его образующей (линии, образующей боковую поверхность конуса). Линия пересечения конуса и плоскости будет параболой. Это хорошо видно на схеме ниже.
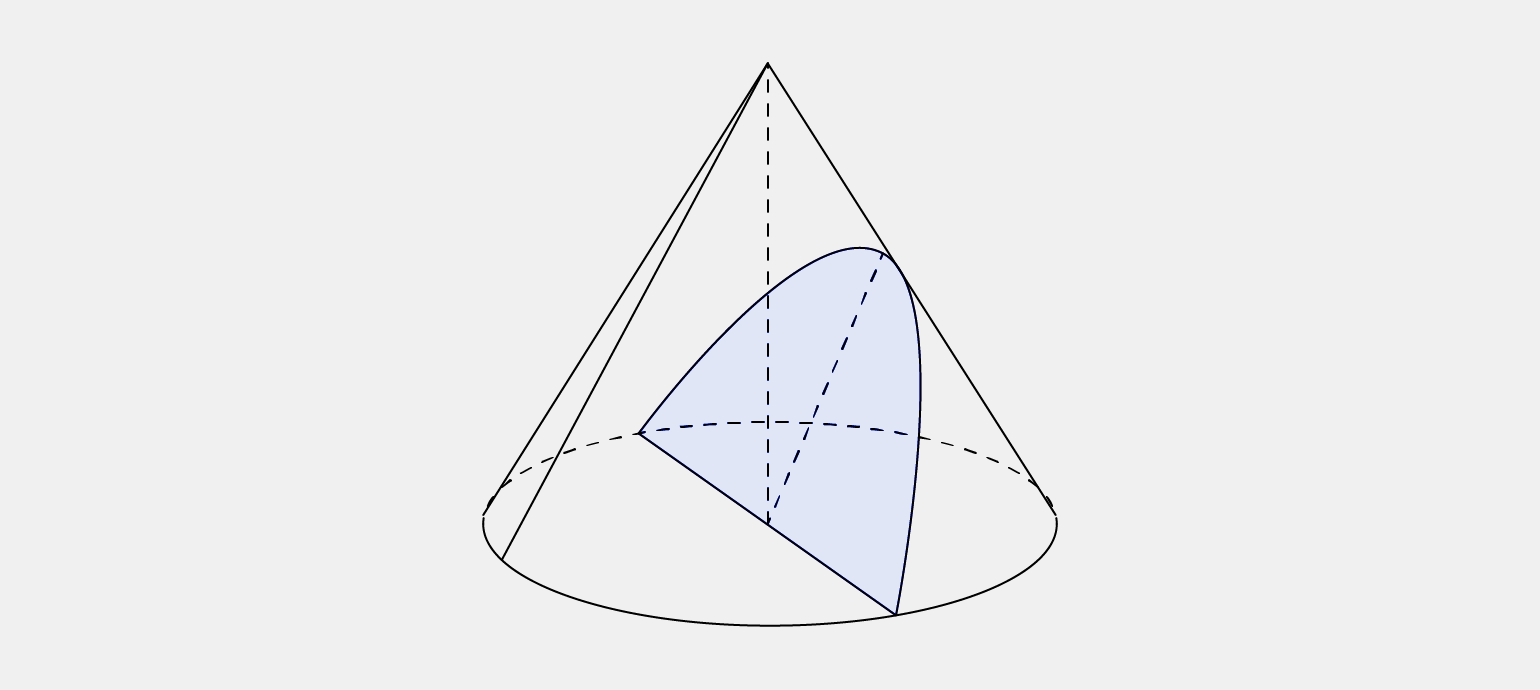
Инфографика: Оля Ежак для Skillbox Media
Внутри параболы находится специальная точка — фокус. Она обладает интересным свойством: все лучи, параллельные оси симметрии и отражённые от параболы, проходят через эту точку.
Представьте себе параболическое зеркало, например отражатель в фонарике. Когда световой луч исходит из фокуса параболы и отражается от её поверхности, он выходит параллельно оси симметрии параболы. Обратное тоже верно: параллельные лучи, попадающие на параболу, будут отражаться в направлении фокуса.
Инженеры часто используют фокус параболы в различных областях. Например, спутниковая тарелка собирает сигнал в точке фокуса, в которой находится специальный приёмник. Также параболические зеркала используются в автомобильных фарах, чтобы направить световой луч прямо на дорогу. Аудиоинженеры применяют параболические поверхности в акустике, чтобы звук, отражаясь, сходился в определённой точке.
Где используются квадратичные функции
Квадратичные функции часто встречаются в повседневной жизни и в науке. Например:
- Траектория движения объекта, брошенного под углом, описывается квадратичной функцией. Так, путь, который описывает мяч, брошенный вверх и падающий обратно на землю, имеет форму параболы.
- Квадратичные функции применяются при проектировании арок и мостов. Им придают параболическую форму, обеспечивающую прочность и устойчивость.
- Квадратичные функции используются для моделирования доходов и затрат в экономике. Например, функция прибыли часто бывает квадратичной, где максимальная прибыль достигается в вершине параболы.
Что запомнить о квадратичной функции
- Квадратичная функция — это функция вида y = ax2 + bx + c, где a, b и c — коэффициенты и a ≠ 0.
- График квадратичной функции — парабола, которая может быть направлена вверх (если a > 0) или вниз (если a < 0).
- Влияние коэффициентов: a определяет ширину параболы и её направление (вверх или вниз), b влияет на смещение параболы по оси X, c определяет точку пересечения с осью Y.
- Вершина параболы — это её наивысшая или наинизшая точка.
- Ось симметрии параболы — это вертикальная линия, проходящая через вершину параболы.
- Пересечение с осью Y находится в точке (0, c).
- Пересечения с осью X — это корни уравнения ax2 + bx + c = 0.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!





