Как найти длину вектора: разбираем 3 способа
Вычисляем по координатам, точкам и теореме косинусов.


Эта статья для новичков, которые хотят познакомиться с векторами. Вы узнаете, что такое вектор, как он обозначается и как рассчитывается его длина. Мы рассмотрим три способа и дополним их формулами, примерами и задачами для закрепления материала.
Содержание
Длина вектора: понятие и основные формулы
Вектор — это направленный отрезок, который имеет начало и конец. Его можно представить как стрелку на карте, указывающую путь от одного города к другому. Расстояние между городами будет длиной вектора, а направление стрелки — его направлением.
Вектор может обозначаться двумя заглавными латинскими буквами со стрелкой сверху или одной строчной латинской буквой. Например, 


Длина, или модуль, вектора — это расстояние между его началом и концом, которое обозначают одной или двумя вертикальными чертами по бокам от его названия. Так, длину вектора 





Модуль вектора может понадобиться для решения различных задач:
- В физике он помогает проанализировать скорость и движение объектов, определить, насколько быстро и куда они движутся.
- В инженерии длина вектора позволяет рассчитать силу и степень её воздействия на объекты, что критично при проектировании и оценке нагрузок.
- В компьютерной графике модуль необходим для определения расстояний между элементами, что важно для их точного отображения и анимирования.
Длину вектора можно определить несколькими способами:
- по координатам вектора:
- по координатам точек:
.
- по теореме косинусов:
.
В следующих разделах мы подробно рассмотрим каждую формулу и на примерах потренируемся вычислять длину вектора.
 — это направленный отрезок с начальной точкой, конечной точкой и длиной
— это направленный отрезок с начальной точкой, конечной точкой и длинойИллюстрация: Skillbox Media
Как найти длину вектора по координатам
Для определения положения точки в пространстве с помощью чисел используется система координат, которая показывает расстояние до определённой оси в этой системе. В двумерной системе координат есть две оси: горизонтальная ось X и вертикальная ось Y. В трёхмерной системе добавляется ось Z, перпендикулярная осям X и Y. Оси служат ориентирами для измерения координат и обычно пересекаются в начальной точке, образуя прямоугольную сетку.
Расположим точку A вектора 
Если мы проведём перпендикуляры из точки B на оси X и Y, то получим два прямоугольных треугольника. На рисунке ниже они будут обозначаться как 



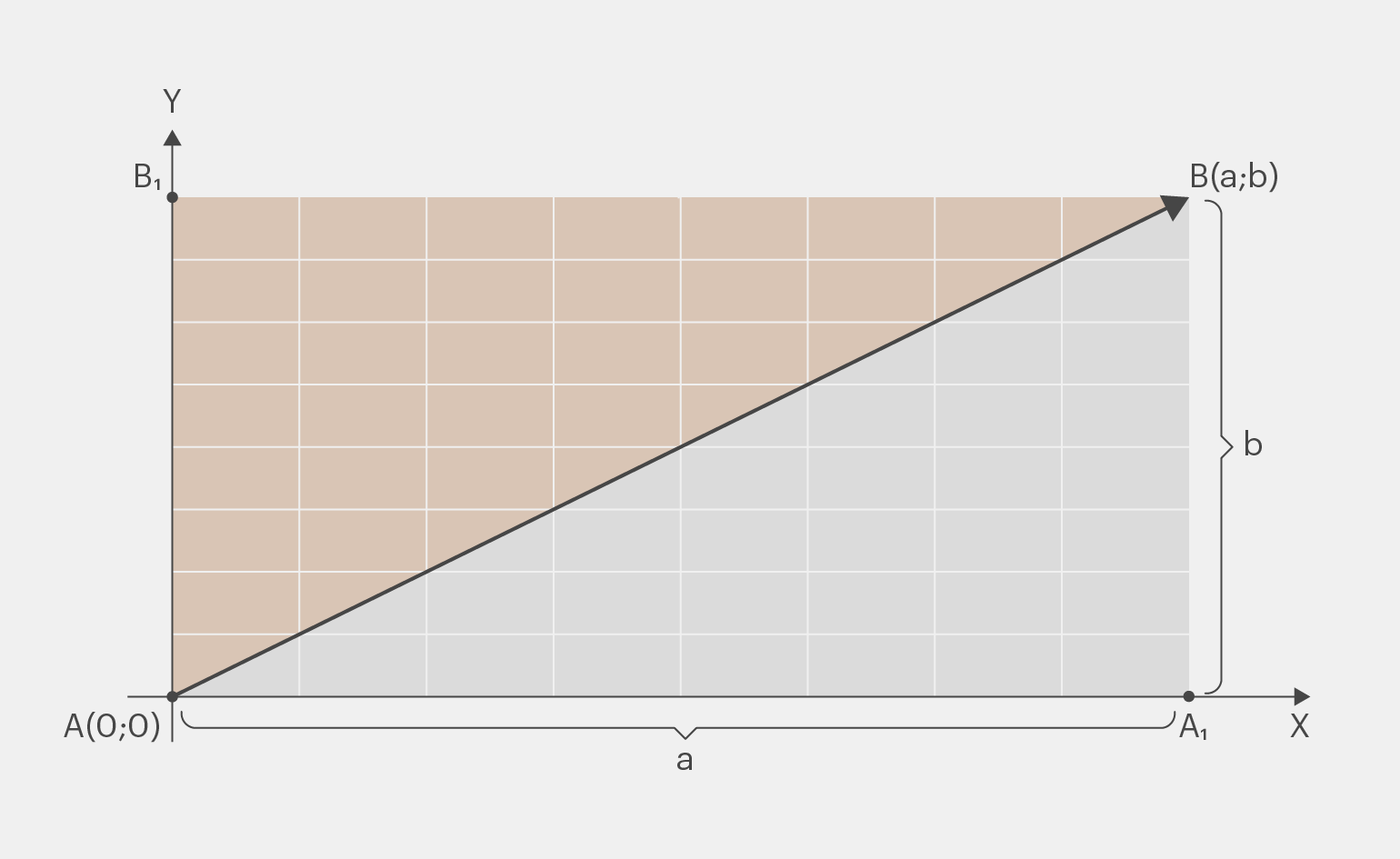
 — гипотенуза прямоугольного треугольника
— гипотенуза прямоугольного треугольника 
Иллюстрация: Skillbox Media
К прямоугольному треугольнику мы можем применить теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Формула: 

Предположим, у нас есть вектор 
Модуль вектора 
Изменим координаты вектора 
Решение
Как найти длину вектора по двум точкам
В предыдущем разделе мы находили длину вектора, исходя из начала координат. Теперь рассмотрим случай, когда вектор задаётся двумя произвольными точками в пространстве.
Предположим, у нас есть некий вектор с начальной точкой (x1, y1) и конечной точкой (x2, y2 ). Чтобы определить длину вектора, сначала нужно найти разность между координатами конечной и начальной точки:
- для координаты X:
;
- для координаты Y:
.
Разности Δx и Δy будут длинами катетов прямоугольного треугольника, гипотенуза которого и будет длиной нашего вектора.
Теперь мы можем вычислить длину вектора по знакомой формуле, основанной на теореме Пифагора для прямоугольного треугольника: 
Вычислим длину вектора 
- для координаты X:
= 7 − 2 = 5;
- для координаты Y:
= 15 − 3 = 12.
Подставляем значения в формулу:
Если нам нужно определить модуль вектора в трёхмерном пространстве, то мы выполняем те же действия, но учитываем дополнительную координату. Попробуйте сами. Пусть у нашего вектора начальная точка (2, 3, 4), а конечная точка (6, 7, 9).
Решение
Определяем разницу между координатами:
= 6 − 2 = 4;
= 7 − 3 = 4;
= 9 − 4 = 5.
Подставляем результаты в формулу:
Как найти длину вектора по теореме косинусов
Иногда мы можем столкнуться с ситуацией, когда несколько векторов образуют треугольник и этот треугольник не является прямоугольным. Если необходимо найти длину вектора, координаты которого нам неизвестны, мы можем использовать теорему косинусов. Это возможно, если нам известны длины двух других векторов и угол между ними.
Теорема косинусов звучит так: «Квадрат длины стороны треугольника равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними».
Таким образом, чтобы найти длину одной из сторон треугольника, нам необходимо:
- рассчитать сумму квадратов длин двух других сторон;
- вычесть из этой суммы удвоенное произведение длин этих сторон на косинус угла между ними;
- извлечь квадратный корень из полученного числа.
Пусть у нас есть треугольник 



- угол α находится напротив стороны
;
- угол β находится напротив стороны
;
- угол γ находится напротив стороны
.
Найдём длину вектора 
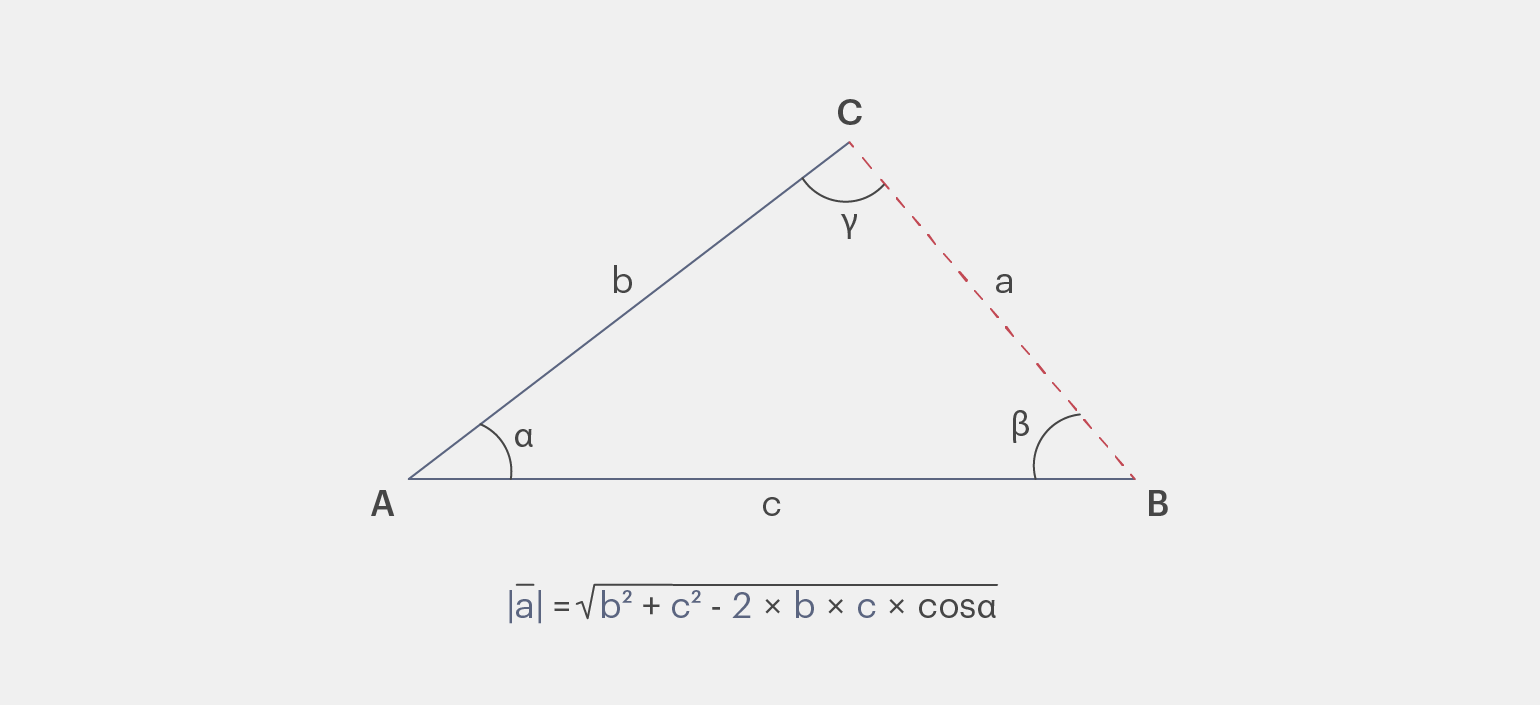
 , образованный тремя векторами, длину одного из которых мы можем вычислить по теореме косинусов.
, образованный тремя векторами, длину одного из которых мы можем вычислить по теореме косинусов. Иллюстрация: Skillbox Media
Допустим, у нас есть следующие данные: модуль вектора 



Попробуйте решить подобную задачу самостоятельно. Исходные данные: модуль вектора 




Решение
Смотрим значение косинуса угла α, который в нашем случае будет таким: 

Вычисления:
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!












