Что такое коллинеарность векторов и как её определить
Простое подробное объяснение с примерами для новичков.


Представьте, что вы разрабатываете приложение для построения маршрутов и хотите оптимизировать пути между зданиями. Программе нужно, например, выяснить, находятся ли библиотека, школа и больница на одной прямой. Если это так, можно избежать ненужных пересечений дорог и поворотов. В решении задачи вам поможет концепция коллинеарности.
Помимо программирования, коллинеарность применяется в линейной алгебре, геометрии, физике и других областях. В этой статье мы разберёмся, что это такое и как её определить.
Содержание
- Первое условие: масштабное соотношение
- Второе условие: равное отношение
- Третье условие: нулевое векторное произведение

Эксперт
Пётр Емельянов
Эксперт Skillbox, CEO в Bloomtech, специалист по информационной безопасности и анализу данных. Опыт в IT — 20 лет.
Что такое коллинеарные векторы
Для знакомства с коллинеарными векторами нужно освежить в памяти два понятия: вектор и нулевой вектор.
Векторы — это направленные отрезки с определёнными началом и концом. Они могут обозначаться двумя заглавными буквами со стрелкой над ними — например, 

Если начало и конец совпадают, то такой вектор называется нулевым. Визуально он выглядит как точка, поскольку не имеет длины и определённого направления. Обозначается нулевой вектор так: 
Теперь, если мы разместим три или более точки на одной прямой, то они будут считаться коллинеарными. Такие точки можно соединить одной прямой линией. Слово «коллинеарность» происходит от латинского слова collineare — «направлять» или «располагать на одной линии».
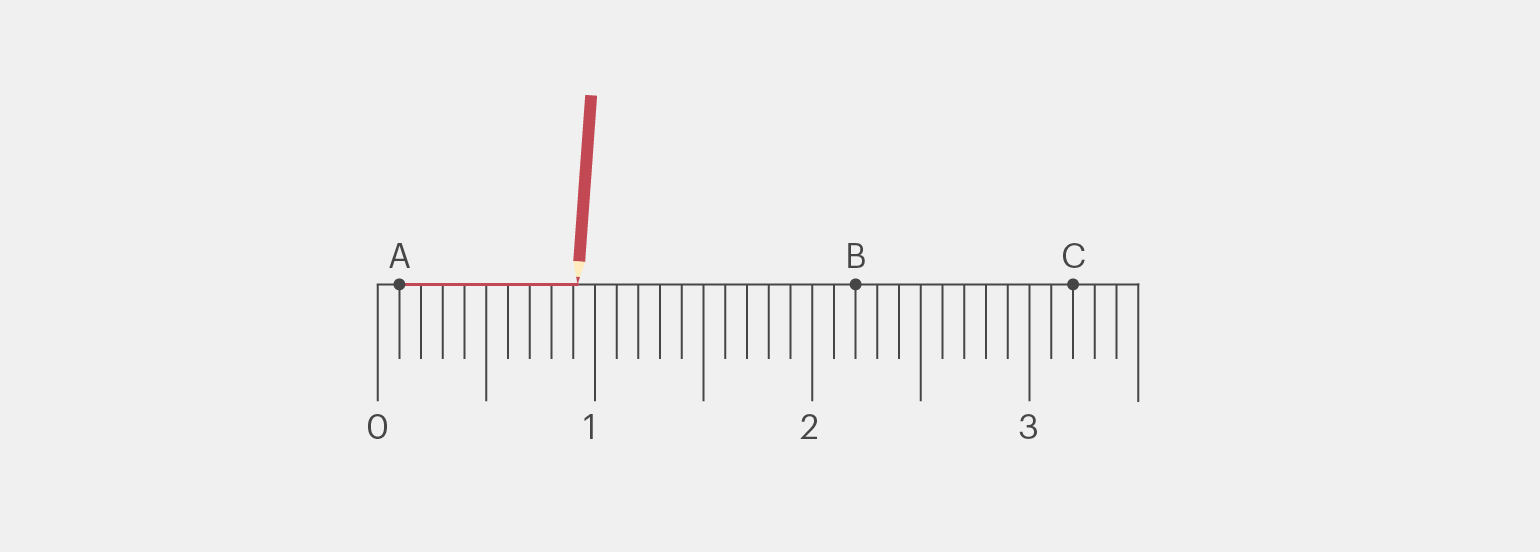
Изображение: Майя Мальгина для Skillbox Media
С векторами немного иначе. Коллинеарными называют два ненулевых вектора, расположенных на одной или параллельных прямых. Нулевой вектор коллинеарен каждому, поскольку считается параллельным любой прямой. Для обозначения коллинеарных векторов используется символ ∥. Например, если 



Коллинеарные векторы могут иметь одинаковую или разную длину, а их направления могут совпадать или быть противоположными. Например, два вектора, указывающие вправо на числовой прямой, коллинеарны. Также коллинеарными будут два вектора, направленные в противоположные стороны: вправо и влево или вверх и вниз. Если коллинеарные векторы имеют одно направление, то они называются сонаправленными. Они могут обозначаться знаком параллельности ∥ или двумя стрелками вверх ↑↑. Примеры записи: 



Если коллинеарные векторы направлены в разные стороны, то их называют противоположно направленными. Их можно обозначить знаком параллельности ∥ и минусом перед вторым вектором — или двумя стрелками в противоположные стороны ↑↓. Примеры: 



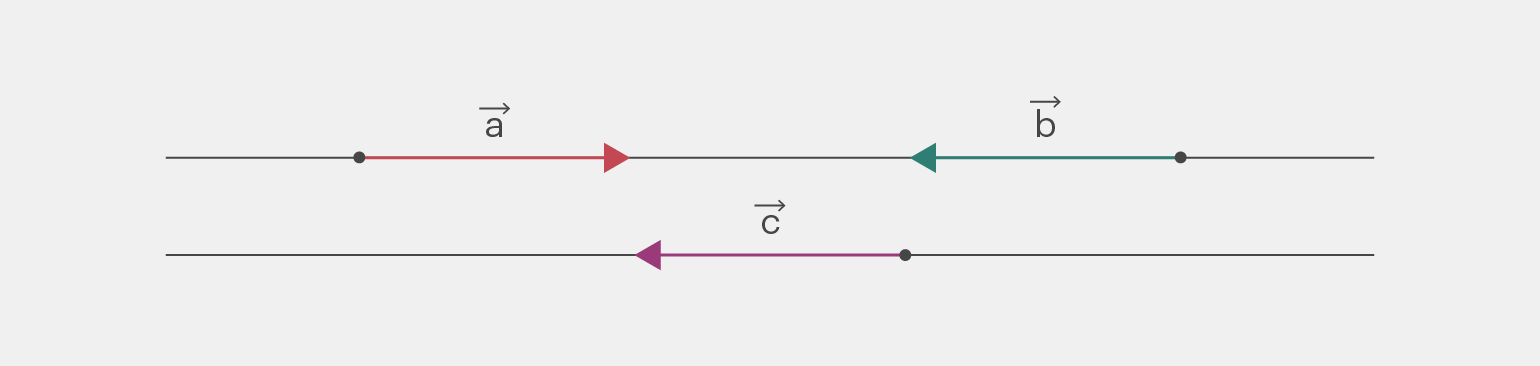
 и
и  — противоположно направленные векторы на одной прямой;
— противоположно направленные векторы на одной прямой; и
и  — противоположно направленные векторы на разных прямых;
— противоположно направленные векторы на разных прямых; и
и  — сонаправленные векторы на разных прямых
— сонаправленные векторы на разных прямыхИзображение: Майя Мальгина для Skillbox Media
Условия коллинеарности векторов
Посмотрите на изображение ниже и найдите пары сонаправленных и противоположно направленных коллинеарных векторов. Скорее всего, благодаря фону в клеточку вы легко справитесь с этой задачей.
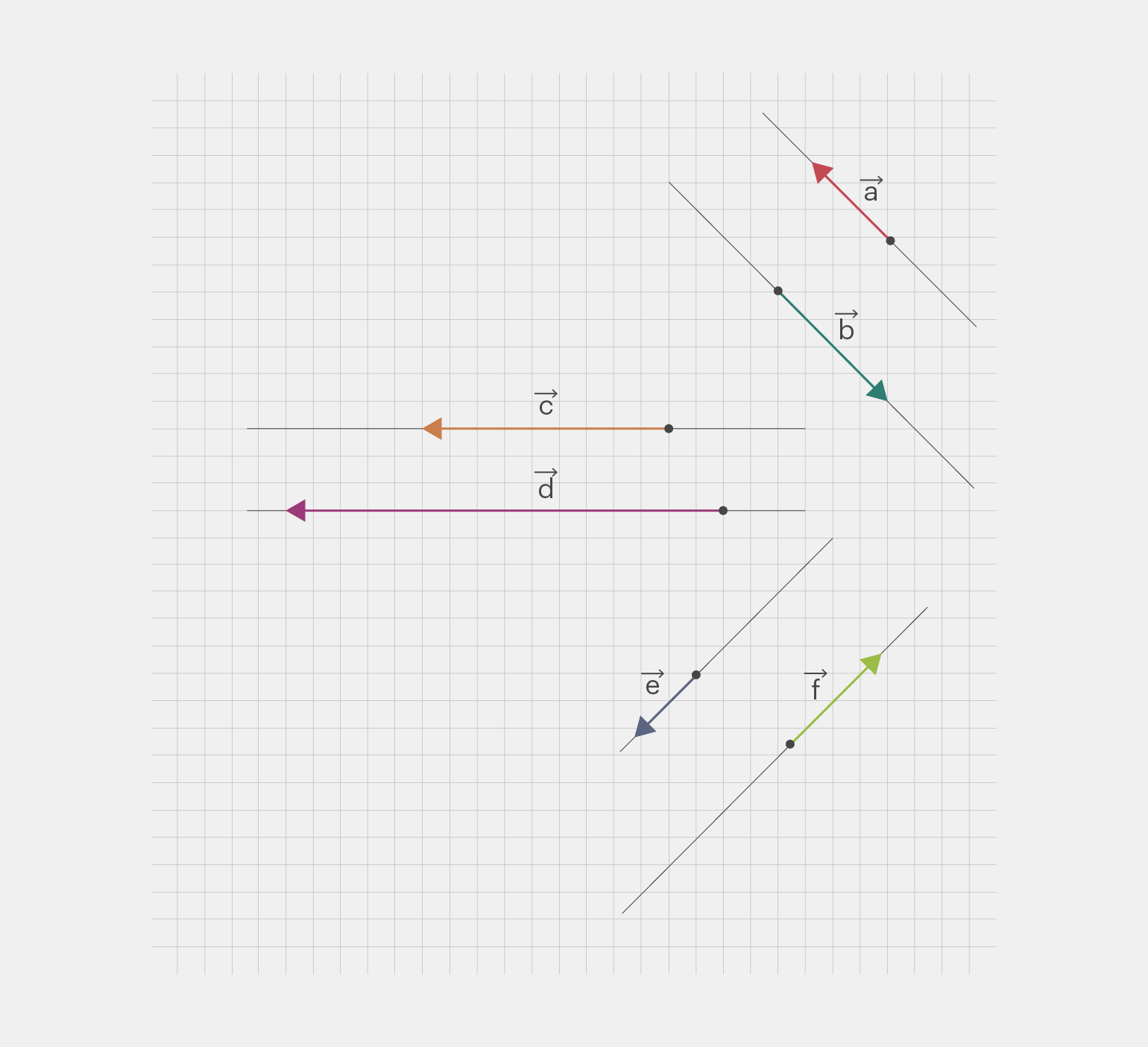
 и
и  — сонаправленные коллинеарные векторы на разных прямых. А вот пары
— сонаправленные коллинеарные векторы на разных прямых. А вот пары  и
и  ,
,  и
и  — противоположно направленные векторы на разных прямых
— противоположно направленные векторы на разных прямых Изображение: Майя Мальгина для Skillbox Media
Если визуально определить коллинеарность векторов не получается, вы можете воспользоваться алгебраическими условиями: масштабным соотношением, отношением координат и векторным произведением. Достаточно, чтобы хотя бы одно из этих условий указывало на коллинеарность.
Первое условие: масштабное соотношение вектора
Векторы 


Предположим, у вектора 

- находим масштабный коэффициент
;
- проверяем, чтобы полученный коэффициент подходил для второй координаты:
.
Если это условие выполняется, то 

Пусть у вектора 


Выполним масштабирование одного вектора в другой.
- проверим первую координату:
;
- проверим вторую координату:
.
Получается, если мы умножим масштабный коэффициент k на координаты вектора 



Теперь попробуйте самостоятельно. У вас есть векторы 

Решение
Определим масштабный коэффициент k для одной из координат на выбор. Например, для x-координаты: 
Проверяем масштабирование координат:
- для x:
;
- для y:
;
- для z:
.
Найденный масштабный коэффициент k позволил преобразовать координаты вектора 




Второе условие: равное отношение координат
Два вектора коллинеарны, если их координаты пропорциональны. В отличие от масштабного соотношения, здесь мы напрямую сравниваем соотношения координат, а не ищем конкретное скалярное число для преобразования одного вектора в другой.
Если векторы 

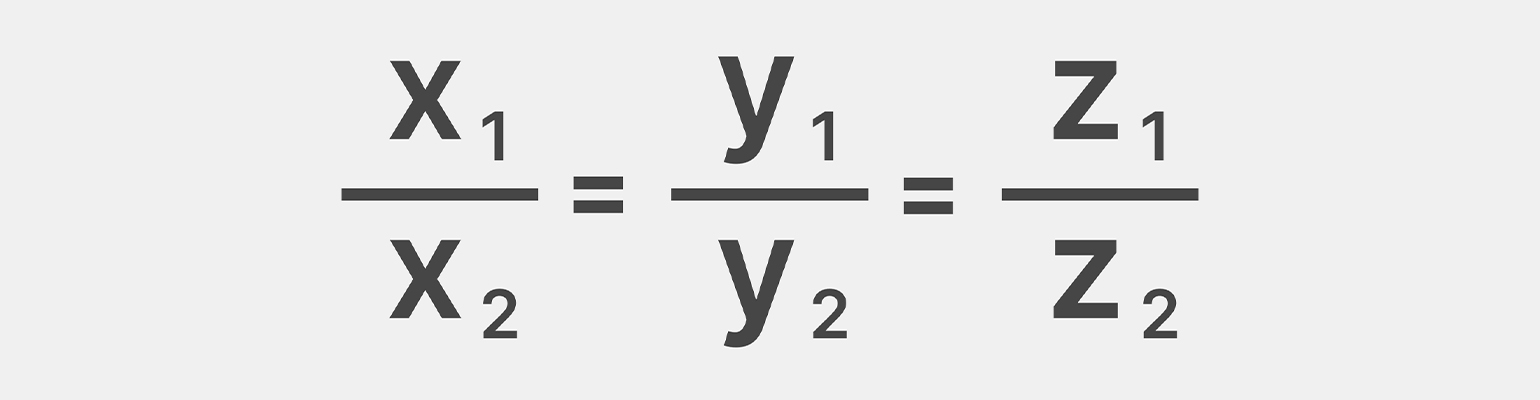
Можно сделать наоборот: разделить координаты второго вектора на координаты первого — здесь, как и в условии масштабного соотношения, это значение не имеет. Перевёрнутая запись будет такой:
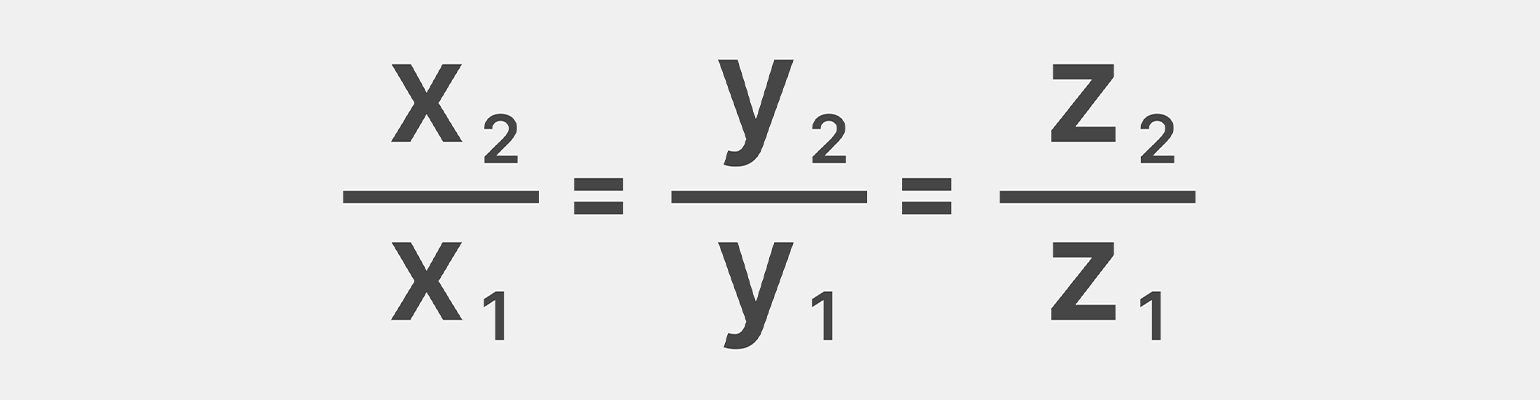
Выберем два вектора в трёхмерном пространстве:

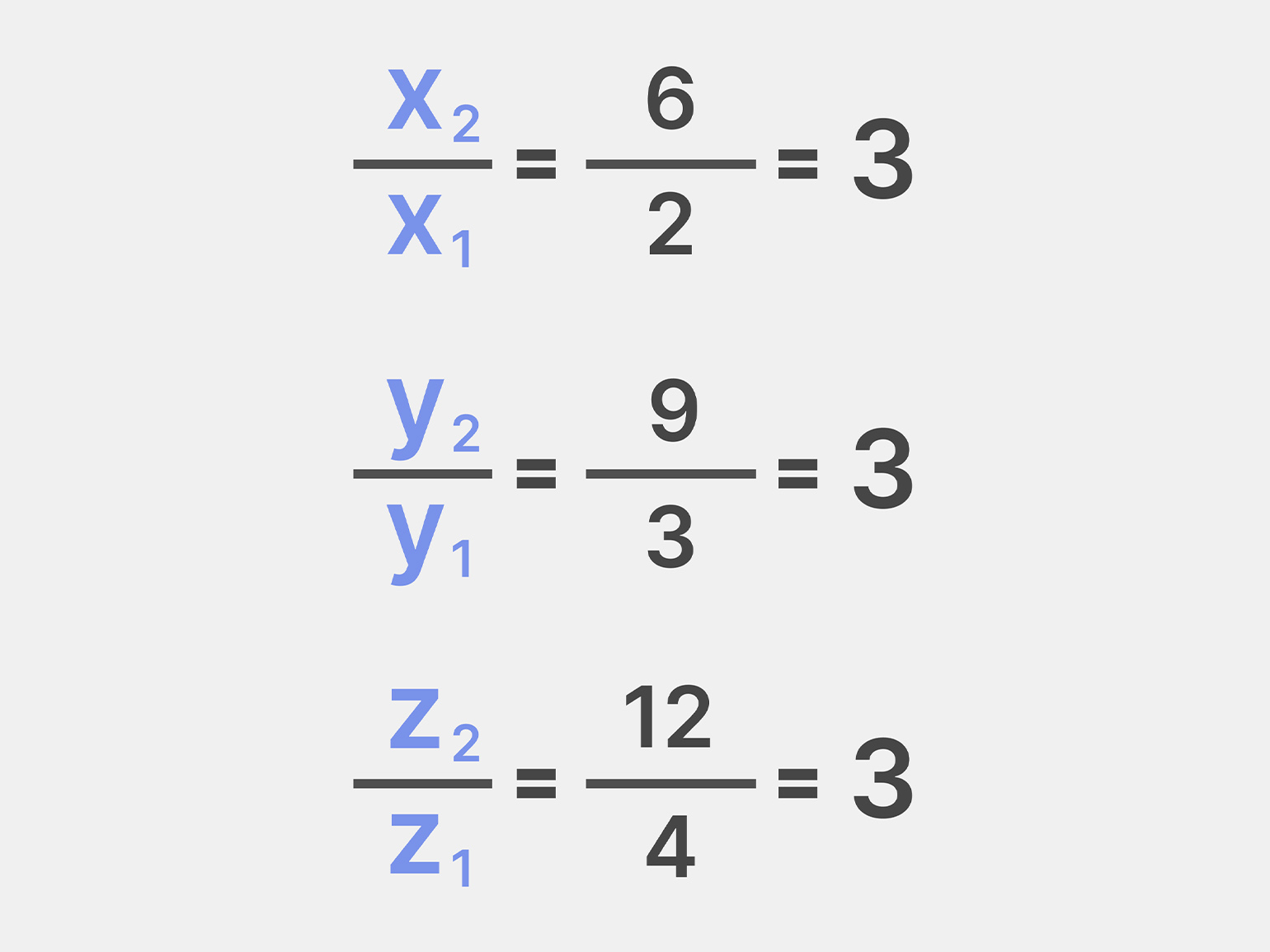
Найденные соотношения равны трём, что подтверждает пропорциональность координат одного вектора координатам другого. Это указывает на то, что

Перейдём к задаче на закрепление. У вас есть два вектора в трёхмерном пространстве: 

Решение
Определяем соотношения для соответствующих координат:
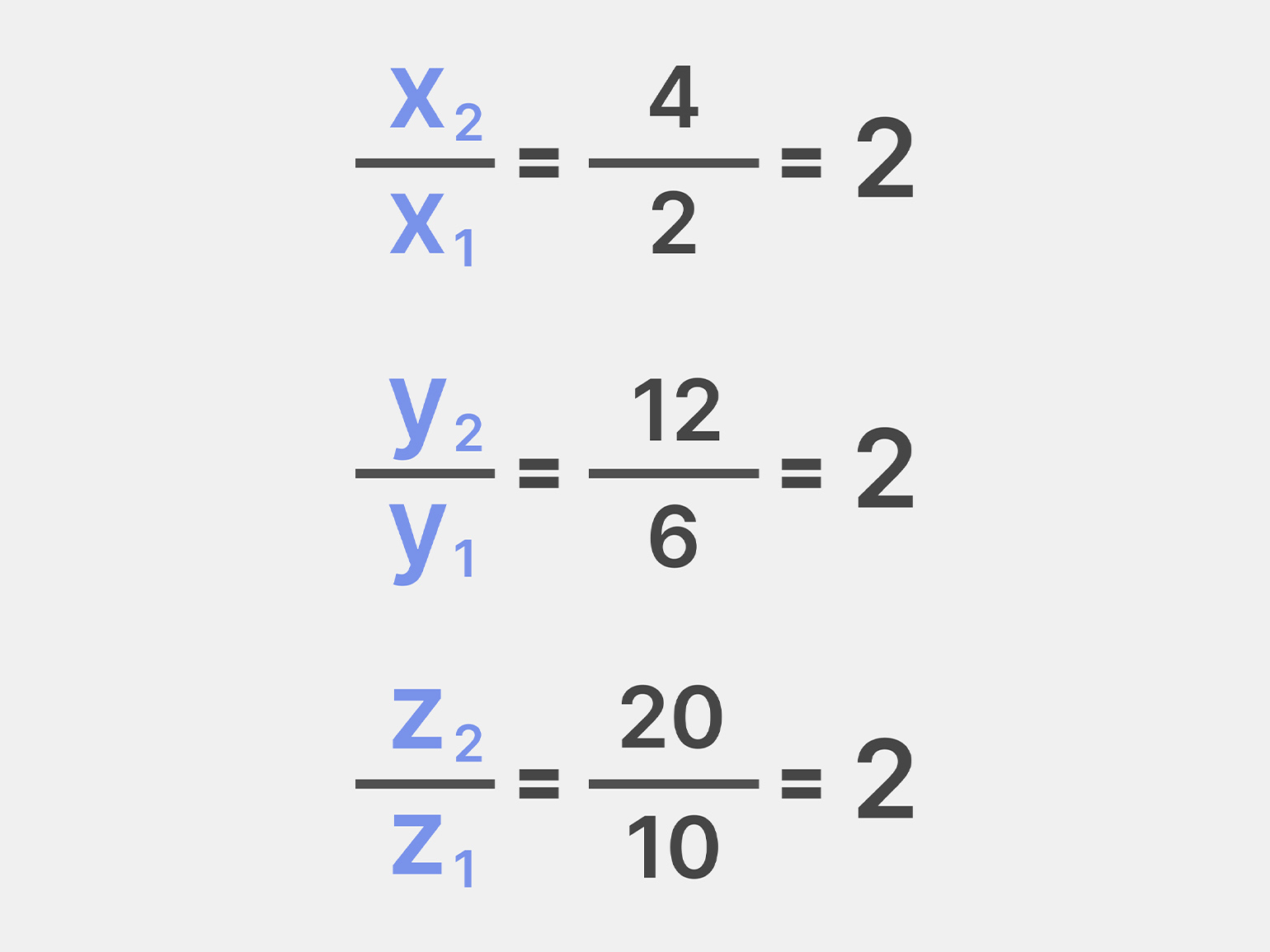
Все найденные соотношения равны двум. Это подтверждает пропорции соответствующих координат и означает, что векторы коллинеарны.
Третье условие: нулевое векторное произведение
Два ненулевых вектора коллинеарны, если их векторное произведение равно нулевому вектору. Этот метод может показаться сложным для новичков, поскольку требует знаний о векторном произведении и умения вычислять определители матриц. Мы объясним этот метод на примере, чтобы вы могли в общих чертах понять его основные принципы.
В общем виде формула для определения коллинеарности двух векторов 






Векторное произведение — это операция с двумя векторами в трёхмерном пространстве, в результате которой получается новый вектор, перпендикулярный обоим исходным векторам. Для наглядности выставьте большой, указательный и средний пальцы на правой руке. Указательный и средний пальцы представляют исходные векторы, а большой палец будет указывать направление вектора, полученного в результате векторного произведения.
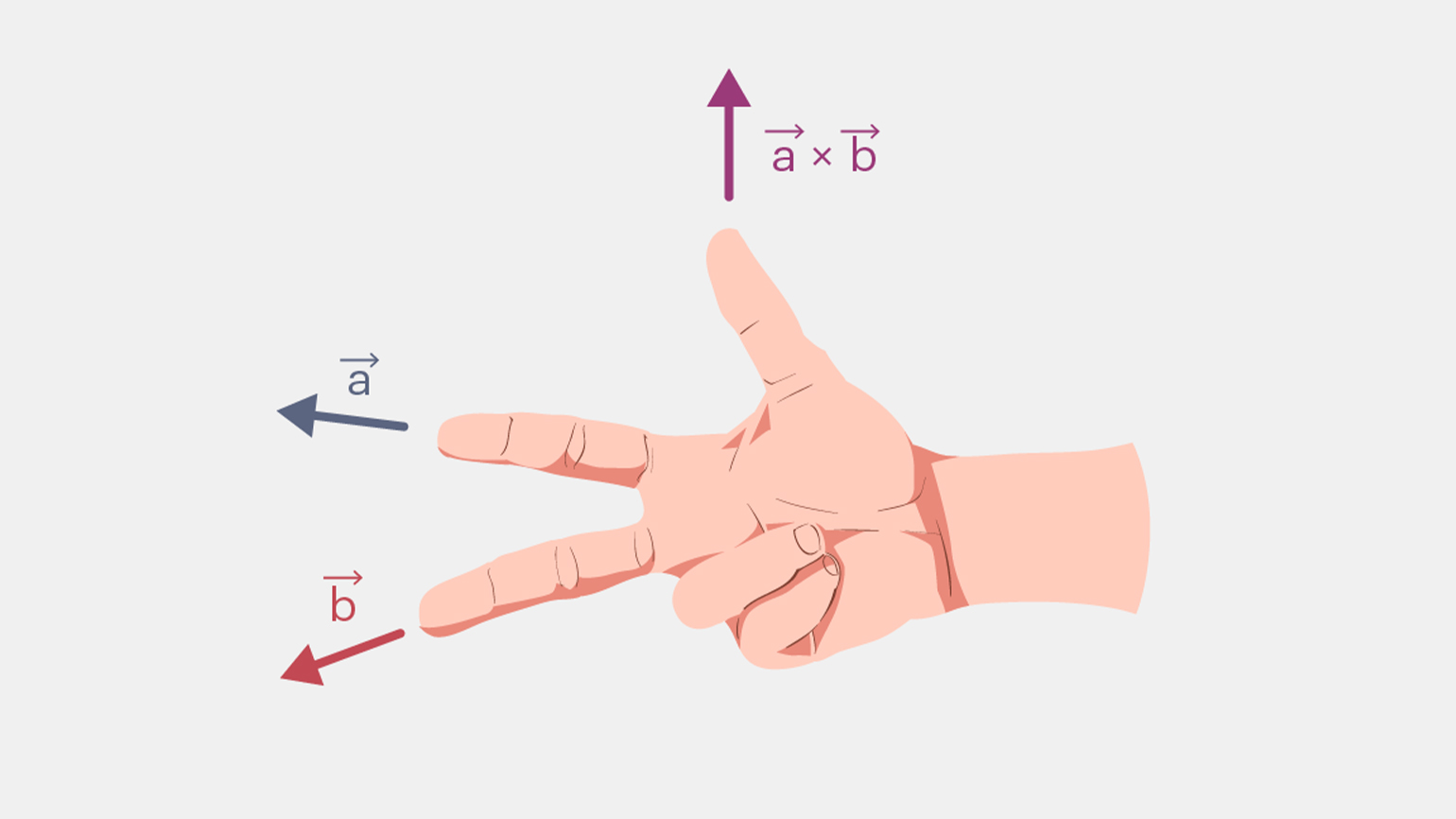
Изображение: Майя Мальгина для Skillbox Media
Для вычисления векторного произведения нужно найти специальное число — определитель, который вычисляется для матрицы с равным количеством строк и столбцов. В нашем случае матрица будет такой:
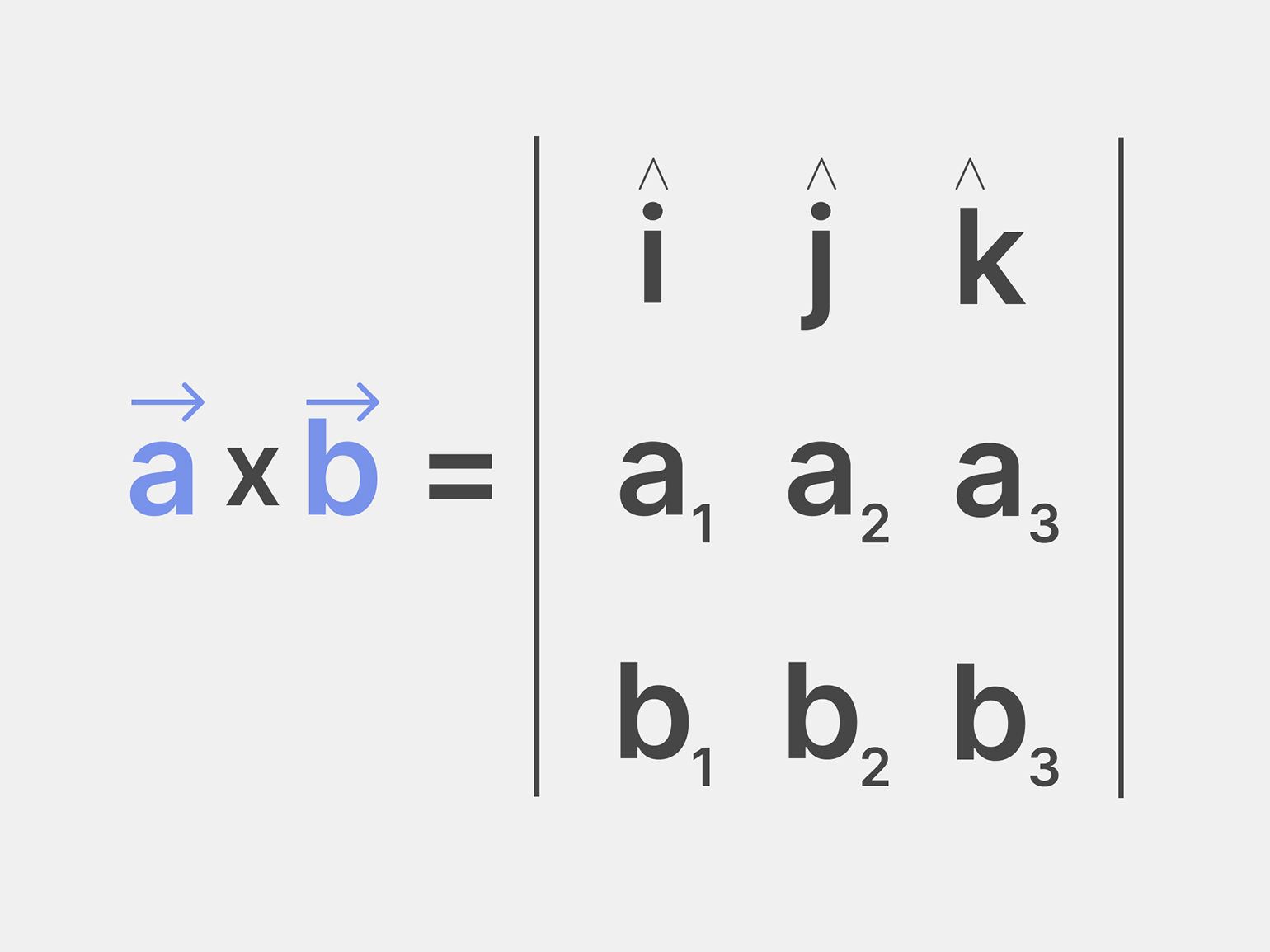
где 


Теперь для получения результирующего вектора используем следующую формулу:

Подставляем координаты наших векторов:

Поочерёдно вычисляем каждую компоненту:
- значение для
:
;
- значение для
:
;
- значение для
:
.
Объединяем компоненты и получаем результат векторного произведения:

Мы получили нулевой вектор, что означает, что 

Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!




