Арифметическая прогрессия: формулы, примеры, определения
Всё, что нужно знать для знакомства с темой.


Представьте, что вы решили еженедельно откладывать по 1000 рублей. Через пять недель у вас будет уже 5000 рублей, за три месяца (12 недель) накопится 12 000 рублей, а через два года (104 недели) сумма достигнет 104 000 рублей. Рассчитать будущие накопления несложно, ведь они растут по правилам арифметической прогрессии.
Арифметическая прогрессия используется в финансовом планировании, статистике, инженерии, программировании и многих других областях, где важно учитывать равномерное распределение величин.
Из статьи вы узнаете:
- что такое арифметическая прогрессия;
- какие у неё основные свойства и формулы;
- чем она отличается от геометрической прогрессии.
Понятие и виды арифметической прогрессии
Арифметическая прогрессия — это последовательность чисел, в которой каждый последующий элемент отличается от предыдущего на одно и то же постоянное значение. Например: 3, 7, 11, 15, 19, 23, 27, … — в этой последовательности каждое число увеличивается на 4 по сравнению с предыдущим.
В математике арифметическую последовательность обозначают строчной буквой a с индексом n внизу: an. Это обозначение указывает на n-й элемент последовательности. Например, первый элемент записывается как a1, второй — как a2 и так далее.
Разность между двумя соседними членами последовательности называется шагом и обозначается буквой d. Шаг можно вычислить по следующей формуле:
d = an + 1 − an, где an — текущий элемент, а an + 1 — следующий элемент последовательности.
В зависимости от значения шага арифметическая прогрессия может быть:
- Возрастающей (если d > 0): каждый член последовательности увеличивается по сравнению с предыдущим. Пример: 2, 5, 8, 11, 14, …
(шаг d = 3). - Убывающей (если d < 0): каждый следующий член уменьшается по сравнению с предыдущим. Пример: 10, 7, 4, 1, −2, … (шаг d = −3).
- Стационарной (если d = 0): все члены прогрессии одинаковы, так как разность равна нулю. Пример: 4, 4, 4, 4, 4, … .
В общем виде арифметическую последовательность можно записать так:
где:
- a1 — первый член последовательности;
- d — шаг последовательности, то есть разность между любыми двумя соседними членами;
- an — n-й член последовательности, который выражается как a1 + (n − 1)d.
Важно отличать арифметическую прогрессию от других типов последовательностей, таких как числовая последовательность и алгебраическая прогрессия.
Числовая последовательность — это упорядоченный набор чисел, каждому из которых присвоен свой порядковый номер. Например, последовательность
2, 4, 6, 8, 10 является числовой с фиксированным шагом, что делает её арифметической прогрессией. Однако существуют и неравномерные числовые последовательности, где шаг меняется произвольно.
Например: 1, 3, 6, 10, 15 — в этой последовательности разности между членами составляют 2, 3, 4 и 5.
Алгебраическая прогрессия — это более общий термин, включающий в себя как арифметические, так и геометрические прогрессии. Этот термин используется для описания любых последовательностей чисел, подчиняющихся определённому алгебраическому правилу.
Основные свойства и формулы арифметической прогрессии
В этом разделе мы рассмотрим основные свойства и ключевые формулы арифметической прогрессии, о которых полезно знать для решения задач.
Характеристическое свойство
Начиная со второго элемента любой член арифметической прогрессии равен среднему арифметическому своих соседей. Это свойство позволяет определить, является ли числовая последовательность арифметической прогрессией:
Обозначим:
- an — n-й элемент прогрессии;
- an − 1 — предыдущий элемент;
- an + 1 — следующий элемент.
Рассмотрим последовательность: 3, 7, 11. Проверим второй член, сравнив его со средним арифметическим первого и третьего членов: (3 + 11) / 2 = 7. Поскольку условие характеристического свойства выполняется, мы имеем дело с арифметической прогрессией.
Формула n-го члена арифметической прогрессии
В арифметической прогрессии разность d между любыми двумя соседними членами постоянна. Это свойство позволяет найти любой элемент последовательности, зная первый член и разность:
Рассмотрим прогрессию 2, 5, 8, 11 с разностью d = 3. Найдём десятый элемент: a10 = 2 + (10 − 1) × 3 = 2 + 9 × 3 = 29.
Формула для нахождения первого члена прогрессии
Если нам известен любой член последовательности, его номер и постоянная разность, то мы можем вычислить первый член:
Пусть элемент с индексом 4 равен 14, а разность d = 3. Подставим эти значения в формулу: a1 = 14 − (4 − 1) × 3 = 14 − 9 = 5.
Разность арифметической прогрессии
Разность d в арифметической прогрессии можно вычислить различными способами, в зависимости от имеющихся данных.
Если известны два последовательных члена прогрессии an и an+1, то разность рассчитывается по формуле:
Например, если два последовательных члена равны 4 и 7, то разность будет такой: d = 7 − 4 = 3.
Если известны два любых члена прогрессии am и an с индексами m и n, разность можно найти по формуле:
Например, если a5 = 7 и a7 = 11, то разность составит: d = (11 − 7) / (7 − 5) = 2.
Если известен первый член a1 и n-й член an, разность можно вычислить, используя формулу для общего члена:
Если a5 = 13 и a1 = 1, то разность будет такой: d = (13 − 1) / (5 − 1) = 3.
Сумма первых n членов арифметической прогрессии
Для нахождения суммы первых n членов арифметической прогрессии можно использовать две формулы в зависимости от того, известен ли последний член последовательности.
Если известен последний член прогрессии, то сумму первых n членов Sn можно вычислить по формуле:
Пусть a1 = 3, an = 15 и n = 5. Найдём сумму первых пяти членов:
Sn = (5 / 2) (3 + 15) = 2,5 × 18 = 45.
Если последний член последовательности неизвестен, то формула будет другой:
Предположим, a1 = 4, d = 2 и n = 6. Найдём сумму первых шести членов:
Sn = (6 / 2) (2 × 4 + (6 − 1) × 2) = 3 × 18 = 54.
Попробуйте решить самостоятельно
Анна решила завести новую привычку — ежедневно читать книги. В первый день она прочитала 20 страниц и планирует каждый день увеличивать количество страниц на 5. Во второй день она должна прочитать 25 страниц, в третий день — 30 страниц и так далее. Попробуйте посчитать, сколько страниц Анна прочитает на 15-й день? А в сумме за 20 дней?
Решение
Из условия задачи мы можем узнать два параметра:
- первый член прогрессии a1 = 20 — это количество страниц, прочитанных в первый день;
- разность прогрессии d = 5 — ежедневное увеличение числа страниц.
Найдём количество страниц, прочитанных на 15-й день. Нам понадобится формула для нахождения n-го члена арифметической прогрессии:
Подставляем значения и считаем: a15 = 20 + (15 − 1) × 5 = 90. Анна прочитает 90 страниц на 15-й день.
Найдём сумму страниц за 20 дней. Здесь нам понадобится формула для нахождения суммы первых n членов арифметической прогрессии:
В нашем случае n = 20 — количество дней, a20 — количество страниц, прочитанных на 20-й день. Сначала найдём a20:
a20 = 20 + (20 − 1) × 5 = 20 + 19 × 5 = 20 + 95 = 115.
Теперь найдём сумму: S20 = (20 / 2) (20 + 115) = 1350.
Анна прочитает в сумме 1350 страниц за 20 дней.
Чем арифметическая прогрессия отличается от геометрической
Вы уже ознакомились с арифметической прогрессией. Теперь давайте кратко рассмотрим геометрическую прогрессию и сравним её с арифметической.
Геометрическая прогрессия — это последовательность чисел, где отношение между любыми двумя соседними членами постоянно. Это отношение называется знаменателем прогрессии и обозначается буквой q. Формула общего члена геометрической прогрессии выглядит следующим образом:
где:
- an — n-й член;
- a1 — первый член;
- q — знаменатель прогрессии.
Рассмотрим геометрическую прогрессию с первым членом a1 = 2 и знаменателем q = 3. Первые несколько членов этой прогрессии будут следующими: 2, 6, 18, 54. В этом примере каждый следующий член получается умножением предыдущего на 3. Например, второй член 6 равен 2 × 3, третий член 18 равен 6 × 3 и так далее.
Легенда о зёрнах на шахматной доске
Когда-то давно индийский мудрец изобрёл шахматы и предложил своему правителю в качестве награды за изобретение насыпать на шахматную доску зёрна риса по особой формуле.
Формула была следующей: одно зёрнышко на первой клетке, два на второй, четыре на третьей и так далее, с удвоением количества зёрен на каждой следующей клетке. Таким образом, количество зёрен росло по экспоненциальному закону.
Когда правитель попытался выполнить просьбу, он обнаружил, что количество зёрен на последних клетках достигает астрономических чисел, которые превышают запасы, собранные со всех рисовых полей в царстве.
Эта история иллюстрирует мощь экспоненциального роста и демонстрирует, как быстро могут увеличиваться числа в геометрической прогрессии.
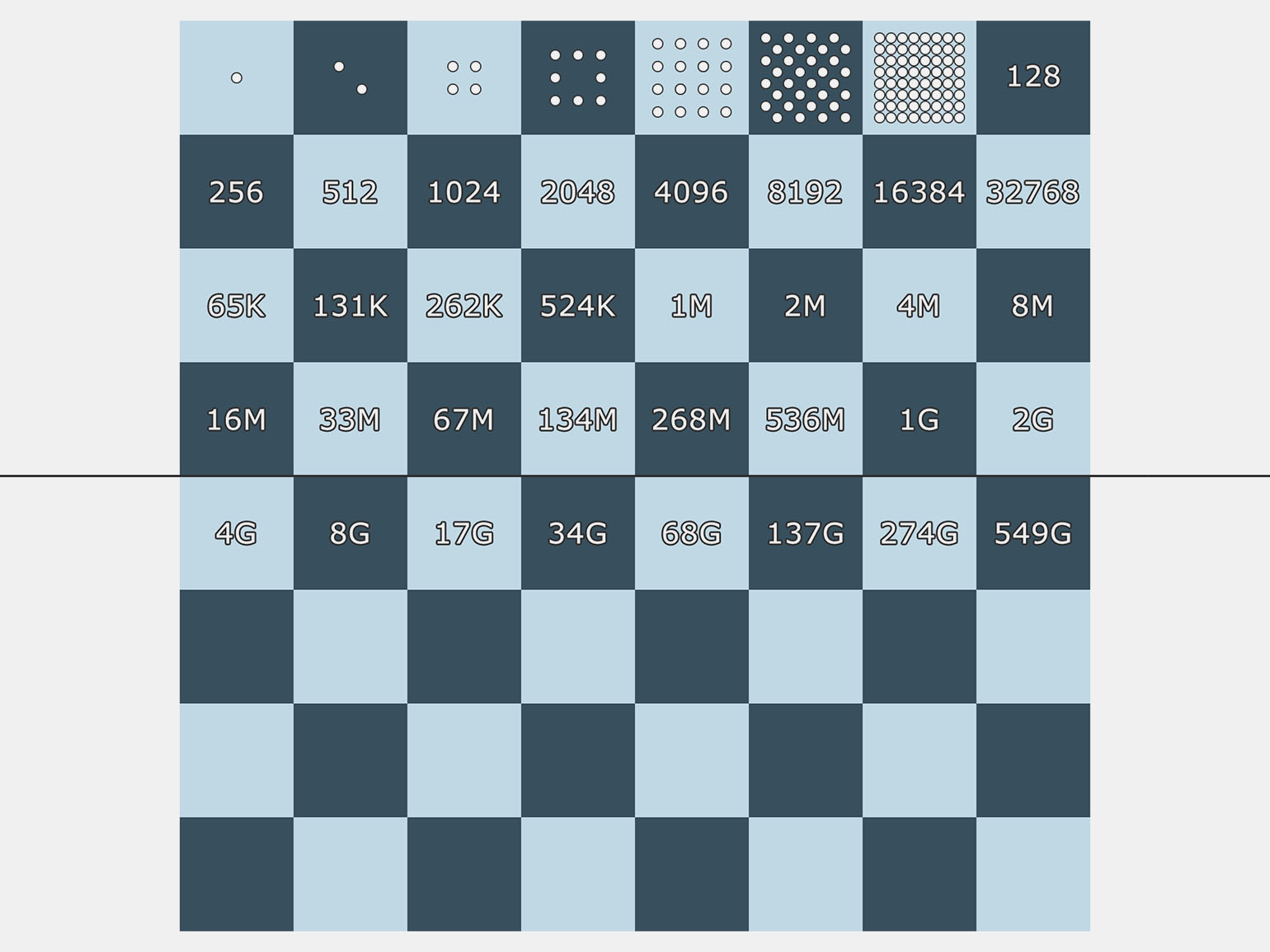
Изображение: Public Domain
Теперь переходим к ключевым различиям:
| Арифметическая прогрессия | Геометрическая прогрессия |
|---|---|
| Каждый последующий член получается добавлением постоянной разности d. Например, в прогрессии 2, 5, 8, 11 каждый следующий член увеличивается на 3. | Каждый следующий член получается умножением предыдущего на постоянный знаменатель q. Например, в прогрессии 2, 6, 18, 54 каждый следующий член получается умножением предыдущего на 3. |
| Основана на линейной формуле, что означает, что разность между членами прогрессии постоянна. Формула для нахождения n-го члена имеет вид an = a1 + (n − 1)d, где d — разность между членами. | Основана на экспоненциальной формуле, что означает, что каждый член прогрессии увеличивается или уменьшается относительно предыдущего. Формула для нахождения n-го члена имеет вид an = a1 × qn − 1, где q — знаменатель прогрессии. |
| Применяется в задачах, связанных с равномерным ростом или уменьшением. Например, в финансовых расчётах, когда нужно рассчитать еженедельные накопления, где каждый новый взнос увеличивается на одинаковую сумму. | Используются там, где процесс характеризуется постоянным процентным изменением. Например, в задачах по сложным процентам, когда нужно вычислить сумму вложений с учётом роста на фиксированный процент в каждом периоде. |
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!














