О нормальном распределении простыми словами

При оценке многих жизненных фактов мы часто сталкиваемся с нормальным распределением. Если кровяное давление вашей бабушки находится в пределах нормы для её возрастной группы, это прекрасно. Однако если ваши оценки по математике соответствуют норме обычной общеобразовательной школы, а вы хотите поступить в МФТИ, то это повод напрячься.

В обоих случаях мы сравниваем показатели с нормой и её границами. Эти нормы не устанавливаются произвольно — их рассчитывают на основании данных большой группы наблюдений. Если распределить эти показатели на графике, то он будет выглядеть примерно так:

Это кривая нормального распределения, о которой мы поговорим в статье. Вы узнаете:

• что такое нормальное распределение;
• какие у него есть свойства и формулы;
• где оно применяется.

Что такое нормальное распределение

В статистике часто используют распределения, чтобы понять, как часто происходят разные события. По сути, распределение — это связь между значением величины и вероятностью того, что она примет это значение.

Например, если мы наблюдаем температуру в Караганде на протяжении года, то распределение может показать, как часто температура принимает значение в том или ином диапазонах. Например, вероятность того, что температура в определённый день будет 25°C, может составлять 10%, а вероятность температуры 30°C — 5%.

Нормальное распределение — это особый тип распределения, при котором большинство значений сосредоточено около среднего. Его также называют гауссовым распределением, законом Гаусса или колоколообразным распределением, а его график — кривой Гаусса, или гауссианой.

В терминах статистики, в нормальном распределении большинство значений находятся в пределах одного среднеквадратического отклонения от среднего (68,2%), двух среднеквадратических отклонений (95,4%), трёх среднеквадратических отклонений (99,7%) и так далее.

Для наглядности позовём бабулю и её подруг. Возьмём распределение показателей кровяного давления у женщин старше 65 лет. Если собрать данные о кровяном давлении большого числа женщин этого возраста, мы увидим, что большинство значений находится в определённом диапазоне, с небольшим количеством значений, сильно отклоняющихся от этого диапазона:

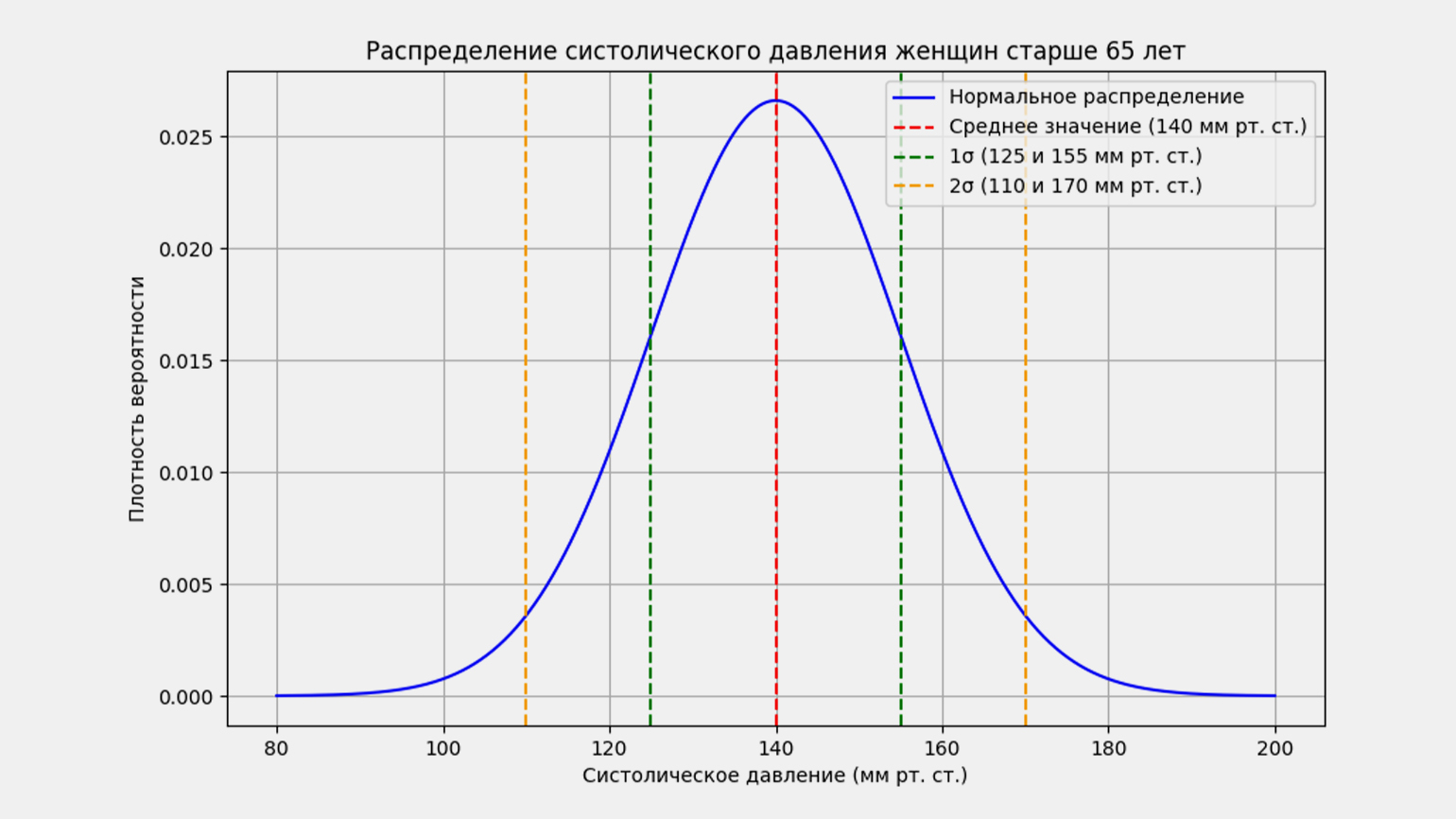
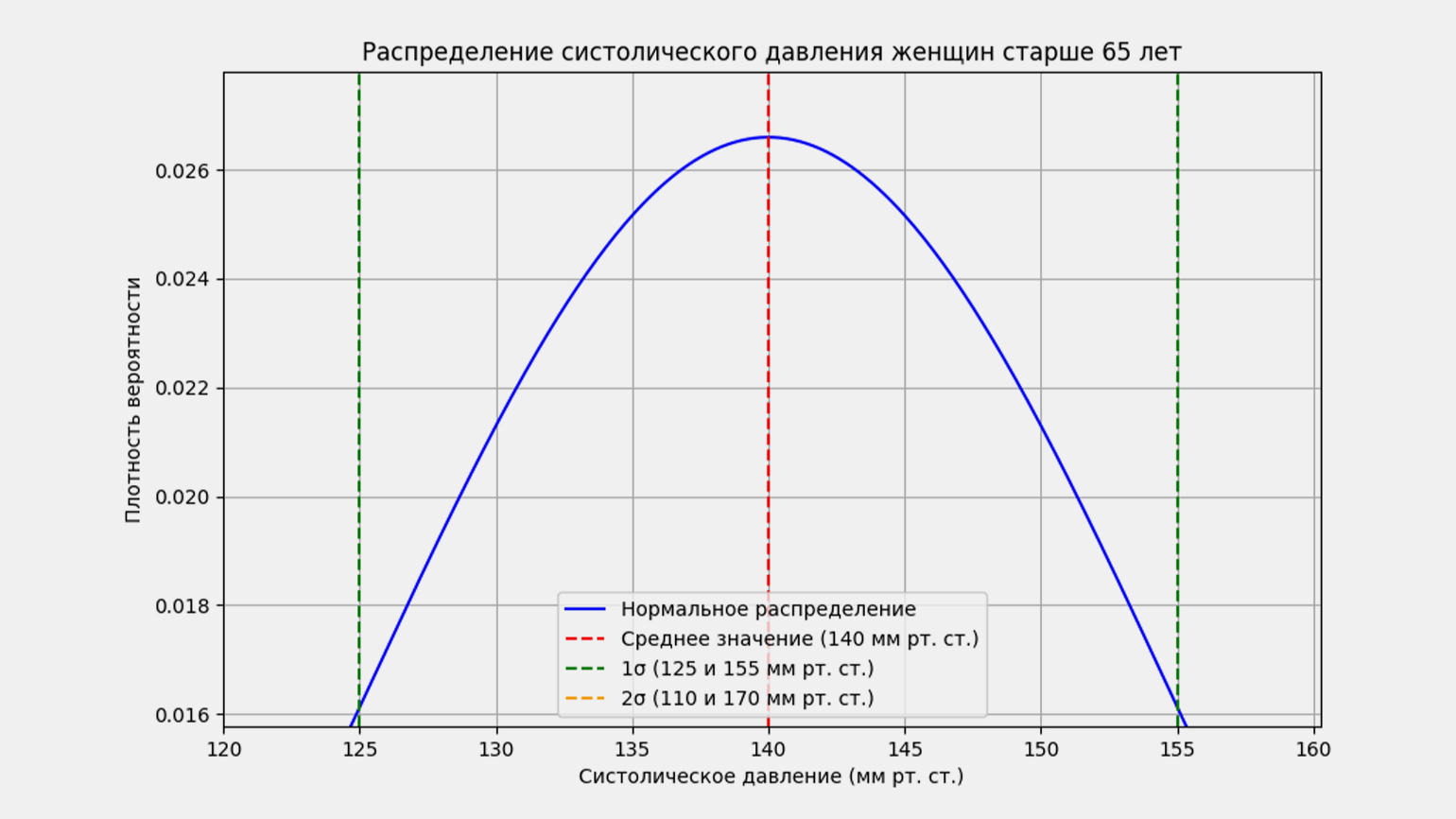
У большинства женщин показатель верхнего давления находится между 125 и 155 — то есть с отклонением в 15 единиц в меньшую или большую сторону от среднего значения, равного 140. Это отклонение называют средним, стандартным или среднеквадратическим отклонением. Его обозначают греческой буквой σ (сигма), а среднее значение обозначают буквой μ (мю):

Закон нормального распределения

Сейчас будет немного страшно:

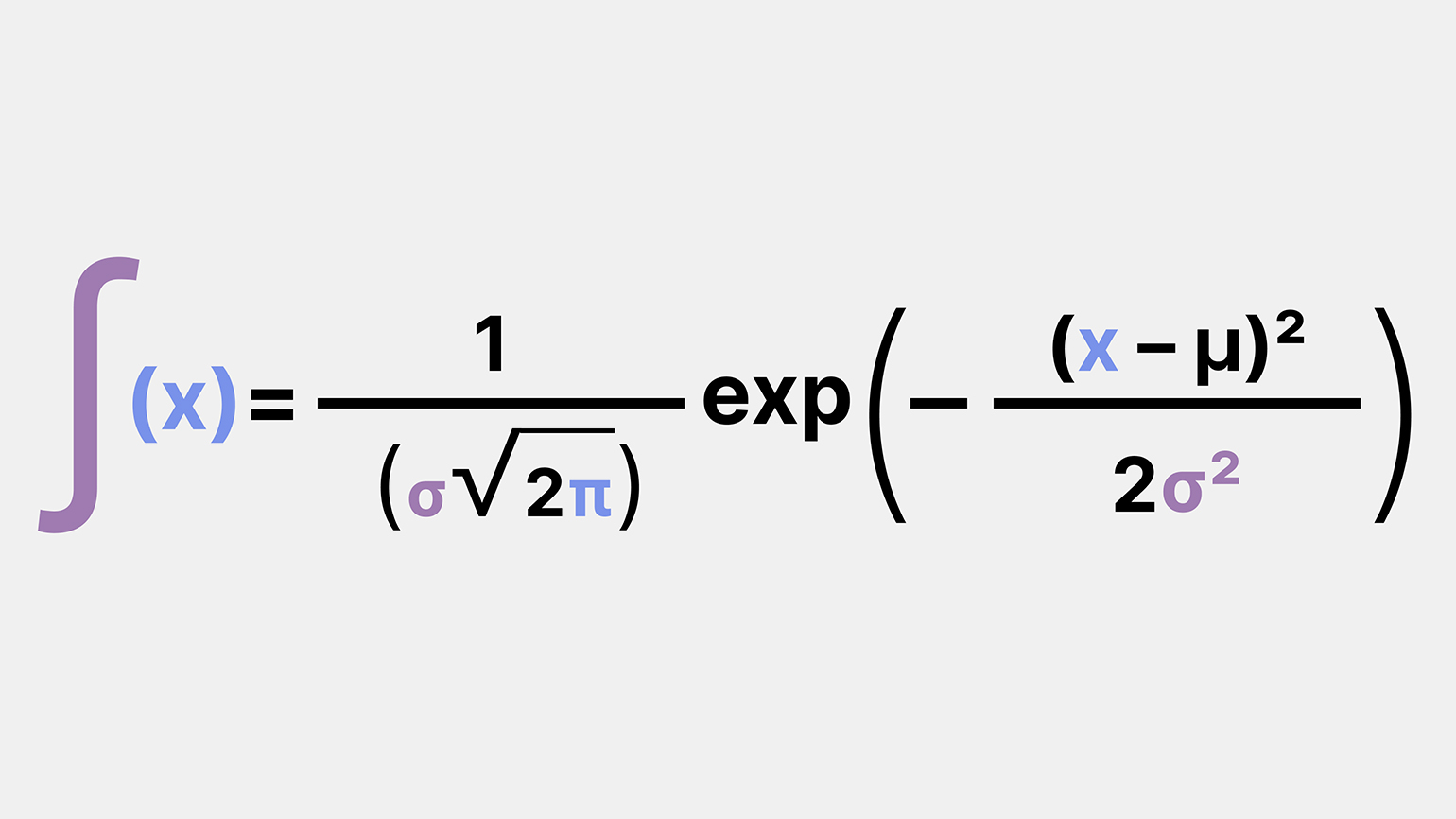
Так выглядит формула закона нормального распределения. Она может показаться сложной, но всё не так страшно. Начнём с того, что нам известно:

• x — это наше значение;
• μ — среднее значение. Его вычислить просто: делим сумму значений на количество;
• σ — стандартное отклонение. Его вычисляют немного сложнее: нужно найти квадратный корень из среднего значения суммы квадратов разностей между каждым значением и средним.

Если мы возведём стандартное отклонение в квадрат, то получим дисперсию. Дисперсия показывает, насколько далеко от среднего значения расположены наблюдения в рамках того или иного распределения:

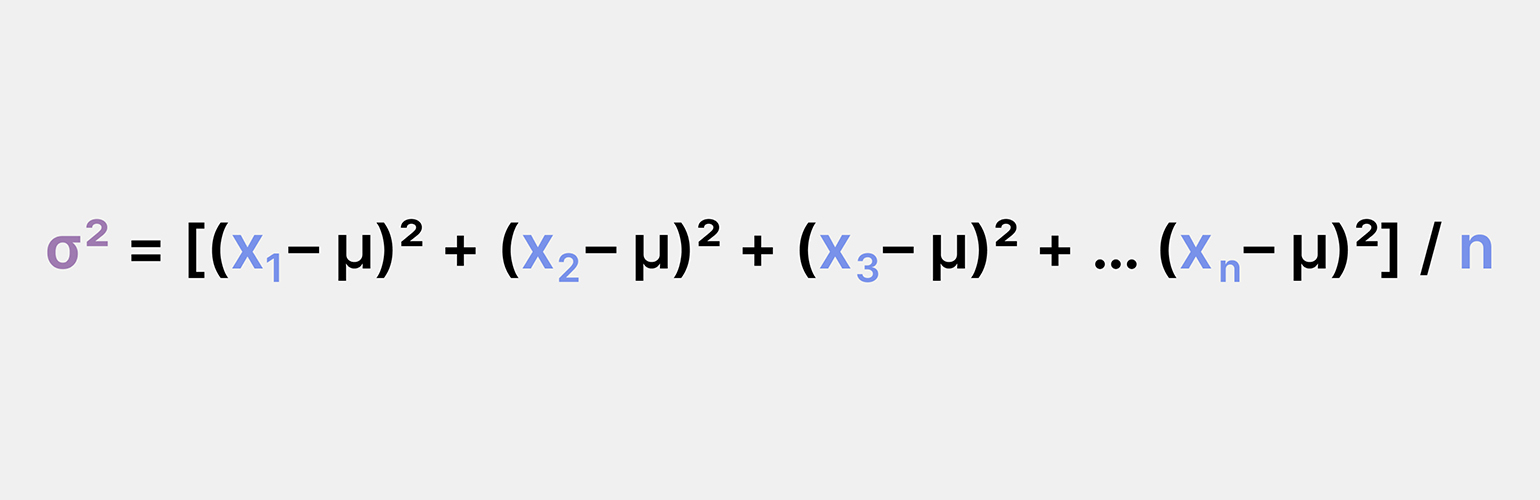
где:

• σ² — дисперсия;
• x₁, x₂, x₃, … x_n — каждое отдельное значение;
• μ — среднее значение;
• n — общее количество значений.

Среднее отклонение равно квадратному корню из дисперсии:

• π — математическая константа пи (≈ 3,14159), которая представляет собой отношение длины окружности к её диаметру;
• exp — функция возведения основания натурального логарифма e (≈ 2,71828) в степень, значение которой указывается в скобках справа.

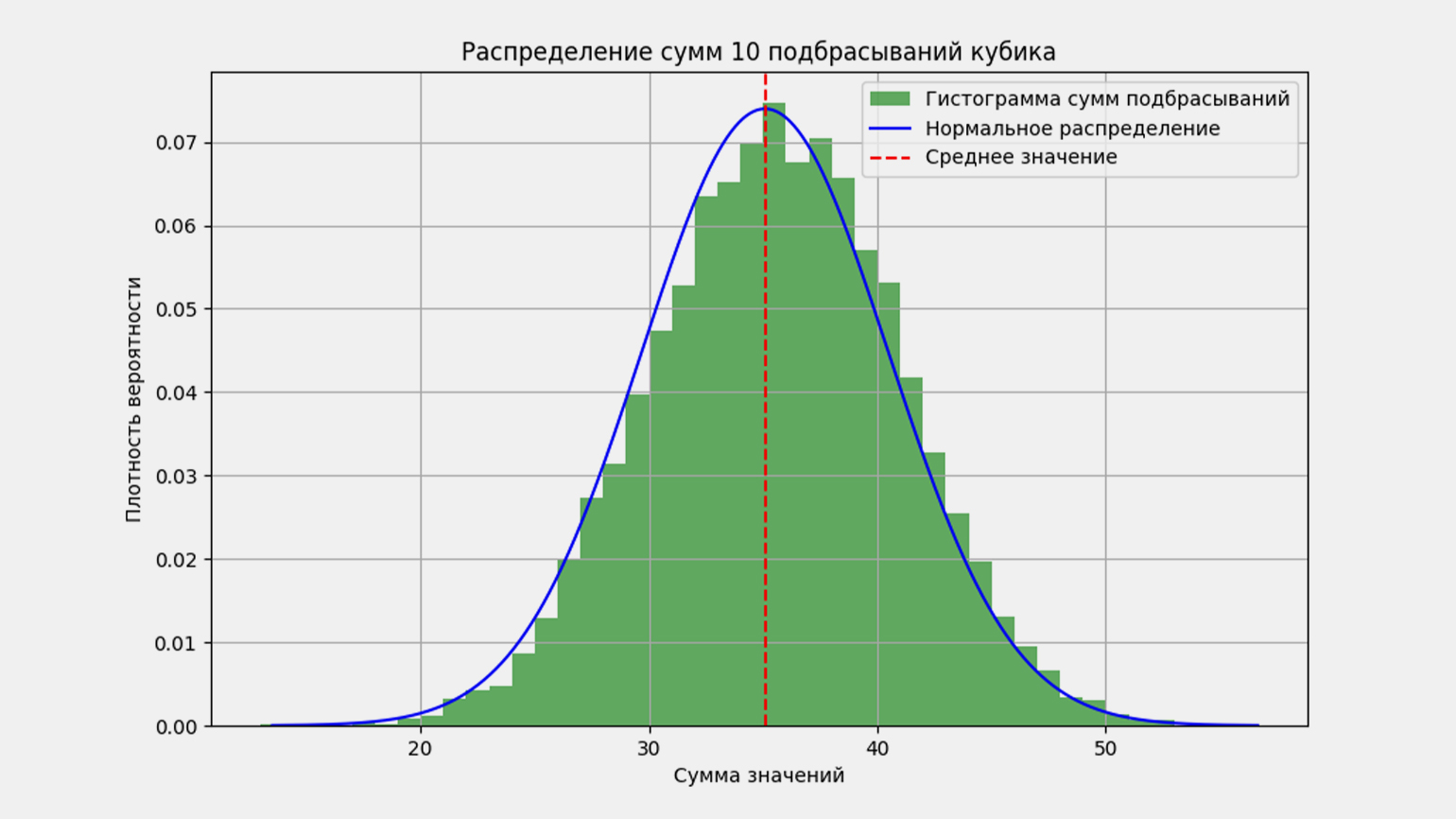
Проверим справедливость формулы на примере подбрасывания игральных костей. Поскольку у нас нет возможности подбрасывать настоящие кубики, мы смоделируем ситуацию, при которой 10 костей подбрасываются одновременно 10 000 раз. Моделирование будем выполнять на Python с использованием библиотек NumPy и SciPy, а график распределения построим с помощью библиотеки Matplotlib.

Если вы умеете работать с Python и его библиотеками, повторите наши действия. Обратите внимание, что в коде используются методы библиотеки NumPy, поэтому ваши конкретные результаты могут немного отличаться. Однако график распределения будет иметь уже знакомую форму — гауссиану:

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# Количество подбрасываний кубика
num_throws = 10000
num_dice = 10  # Количество кубиков, подбрасываемых за раз

# Моделирование подбрасываний кубика
np.random.seed(0)
rolls = np.random.randint(1, 7, size=(num_throws, num_dice))
sums = rolls.sum(axis=1)

# Расчёт среднего и стандартного отклонения
mu = np.mean(sums)
sigma = np.std(sums)

# Создание массива значений
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 1000)
pdf = stats.norm.pdf(x, mu, sigma)

# Построение гистограммы и графика нормального распределения
plt.figure(figsize=(10, 6))
plt.hist(sums, bins=30, density=True, alpha=0.6, color='g', label='Гистограмма сумм подбрасываний')
plt.plot(x, pdf, label='Нормальное распределение', color='blue')

# Добавление вертикальной линии для среднего значения
plt.axvline(mu, color='red', linestyle='--', label='Среднее значение')

# Добавление легенды
plt.legend()

# Добавление заголовка и подписей осей
plt.title('Распределение сумм 10 подбрасываний кубика')
plt.xlabel('Сумма значений')
plt.ylabel('Плотность вероятности')

# Отображение графика
plt.grid(True)
plt.show()

Результат выполнения кода:

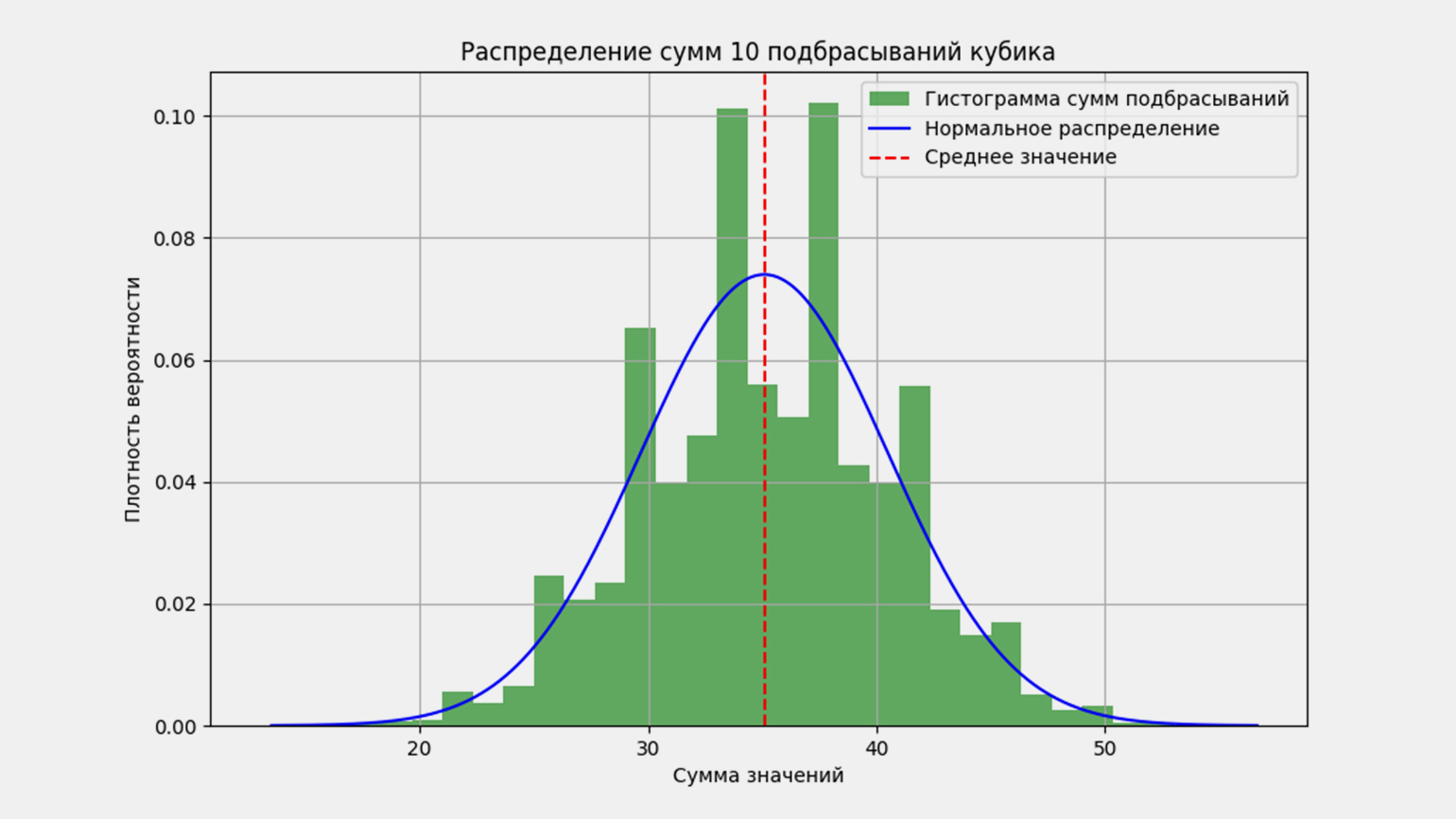
Давайте проверим формулу. Если у вас нет под рукой ручки и бумаги, воспользуйтесь нашим кодом:

import numpy as np

num_throws = 10000
num_dice = 10

np.random.seed(0)
rolls = np.random.randint(1, 7, size=(num_throws, num_dice))
sums = rolls.sum(axis=1)

mu = np.mean(sums)
sigma = np.std(sums, ddof=1)  

print(f"Среднее значение (μ): {mu}")
print(f"Стандартное отклонение (σ): {sigma}")

Мы получили μ = 35 и σ = 5,402. Используем калькулятор OwlCalculator для проверки. Подставляем значения в калькулятор, выбрав любое значение x в пределах от 10 до 60. В нашем примере возьмём значение 32. Калькулятор покажет значение функции плотности вероятности для выбранного x:

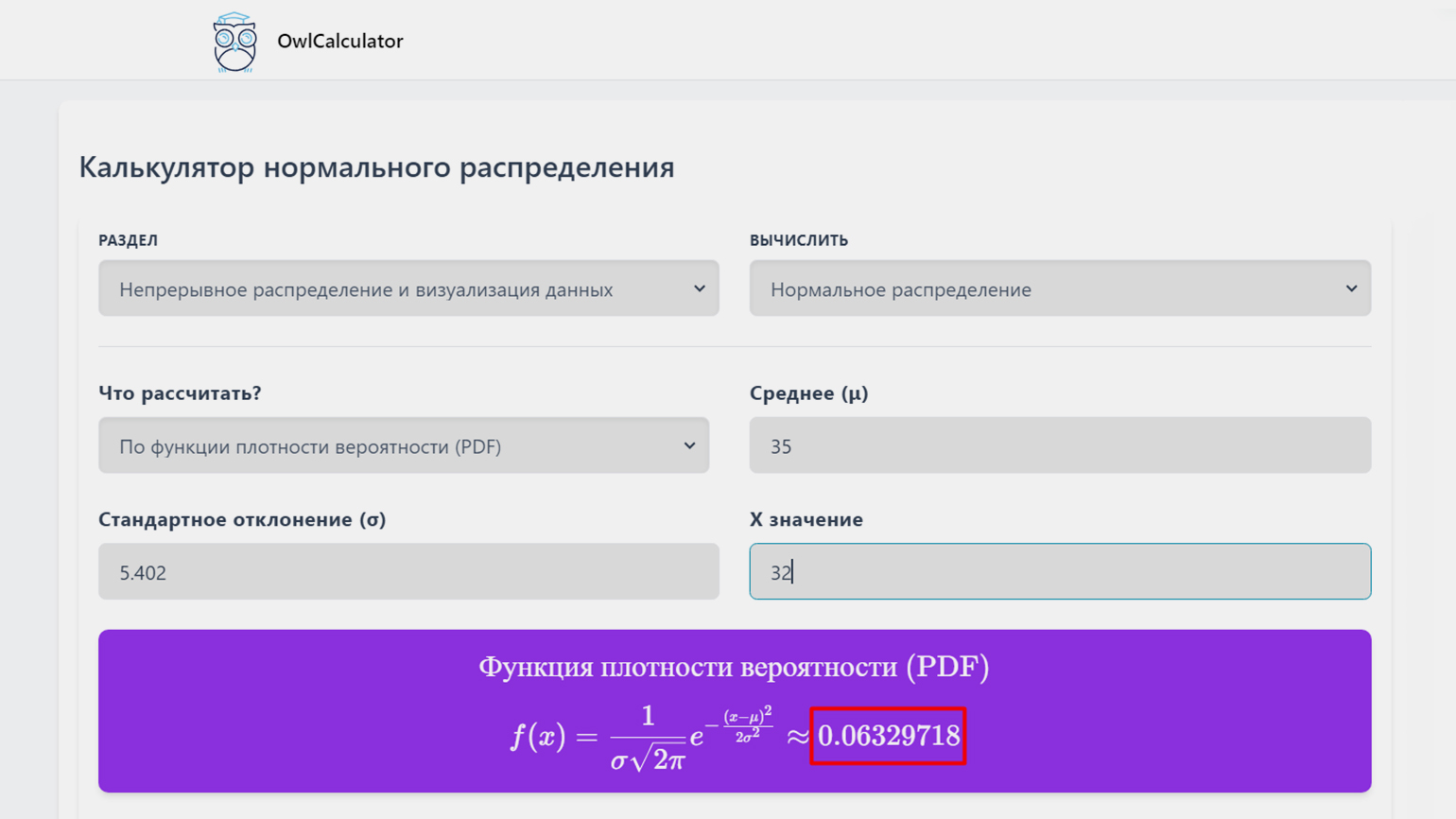
Точно сказать сложно, но приблизительно это соответствует графику. Построим гистограмму с меньшим масштабом, чтобы проверить:

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

num_throws = 10000
num_dice = 10

np.random.seed(0)
rolls = np.random.randint(1, 7, size=(num_throws, num_dice))
sums = rolls.sum(axis=1)

mu = np.mean(sums)
sigma = np.std(sums)

x = np.linspace(mu - 4*sigma, mu + 4*sigma, 1000)
pdf = stats.norm.pdf(x, mu, sigma)

# Границы корзин для гистограммы с шагом 1
bins = np.arange(sums.min(), sums.max() + 1, 1)

# Построение гистограммы и графика нормального распределения
plt.figure(figsize=(10, 6))
count, bins, ignored = plt.hist(sums, bins=bins, density=True, alpha=0.6, color='g', label='Гистограмма сумм подбрасываний')

plt.plot(x, pdf, label='Нормальное распределение', color='blue')

# Добавление вертикальной линии для среднего значения
plt.axvline(mu, color='red', linestyle='--', label='Среднее значение')

plt.legend()

plt.title('Распределение сумм 10 подбрасываний кубика')
plt.xlabel('Сумма значений')
plt.ylabel('Плотность вероятности')

plt.grid(True)
plt.show()

Здесь мы уже лучше видим, что значение гистограммы примерно соответствует результату из калькулятора:

Читайте также:

Начинаем программировать на Python

Примеры нормального распределения

Закон распределения Гаусса хорош своей универсальностью, а примеры его применения можно встретить в различных сферах. Например, в маркетинге. Представьте, что вы менеджер интернет-магазина и хотите понять, как распределяются суммы покупок клиентов. Это поможет вам оптимизировать маркетинговую стратегию и эффективно распределить целевую рекламу.

Вы собираете данные о суммах покупок всех клиентов за последний месяц. Допустим, у вас есть данные о 1000 покупок. Теперь рассчитываем среднее значение и стандартное отклонение сумм покупок. В качестве гипотезы предполагаем, что суммы покупок следуют нормальному распределению с рассчитанными μ и σ.

В результате вычислений оказалось, что средний чек равен 5000 рублей, а стандартное отклонение составляет 1000 рублей.

Теперь используем эти данные. Установим контрольные границы, например ±2σ от среднего значения, что охватывает около 95% всех наблюдаемых значений в нормальном распределении. В нашем случае это будут границы от 3000 до 7000 рублей.

На основании расчётов дадим отделу маркетинга такие указания:

• Если клиент тратит больше 7000 рублей, его можно считать высокоценным и стоит направить на него больше маркетинговых усилий.
• Если клиент тратит меньше 3000 рублей, то это указывает на возможность улучшения маркетинговых стратегий для увеличения среднего чека.

Теперь ребята из отдела маркетинга настроят рекламу так, чтобы большая часть бюджета тратилась на привлечение высокоценных клиентов. Это поможет эффективно использовать рекламные средства и избежать их пустой траты.

Маркетингом сфера применения распределения Гаусса не ограничивается. Оно применяется во многих других областях — от финансов до биологии, помогая анализировать данные и принимать решения на основе статистики:

• в физике — для описания случайных ошибок измерений;
• в биологии — для описания распределения размеров, веса и других характеристик популяций;
• в психологии — для описания распределения IQ и других психологических показателей;
• в экономике — для моделирования распределения доходов, цен и других экономических показателей;
• в демографии — для анализа роста численности населения;
• в инженерном деле — для контроля качества продукции;
• в статистическом контроле процессов — для мониторинга производственных параметров;
• в исследованиях — для обработки результатов экспериментов и опросов;
• в методах оценки и аппроксимации — для предсказания значений на основе известных данных и упрощения сложных функций или распределений.

Что запомнить

• Нормальное распределение (распределение Гаусса, колоколообразное распределение) — это тип распределения, при котором большинство значений сосредоточено около среднего значения.
• Среднее значение μ (мю) и стандартное отклонение σ (сигма) определяют форму кривой нормального распределения (гауссианы).
• По закону нормального распределения 68,2% значений находятся в пределах одного σ от μ, 95,4% — в пределах двух σ, а 99,7% — в пределах трёх σ.
• Зная среднее значение и стандартное отклонение распределения, можно устанавливать контрольные границы и принимать решения на их основе.
• Нормальное распределение широко применяется в различных областях: естественных науках (физика, биология), социальных науках (экономика, демография), психологии, производственных процессах, исследованиях и анализе данных.