Модуль random в Python
Познаём случайные числа и учимся их генерировать.


Это статья для начинающих программистов, которые изучают математику в Python и дошли до модуля random. Мы объясним, как он устроен и где используется, а также из каких функций состоит. После объяснения будет подборка проектов для желающих изучить работу с библиотекой на практике.
Содержание
- Для чего нужен модуль random в Python
- Как работает генерация случайных чисел в Python
- Функции модуля random
- random.random(): возвращает число с плавающей точкой в диапазоне 0.0 <= N < 1.0
- random.uniform(a, b): возвращает число с плавающей точкой в диапазоне a <= N <= b
- random.randint(a, b): возвращает целое число в диапазоне a <= N <= b
- random.randrange(start, stop, step): возвращает целое число в заданном диапазоне с учётом шага
- random.choice(seq): возвращает случайный элемент из последовательности
- random.sample(population, k): выбирает случайные элементы из коллекции
- random.shuffle(seq): в случайном порядке перемешивает последовательность элементов
Для чего нужен модуль random в Python
Модуль random в Python предназначен для генерации псевдослучайных чисел. В этом разделе мы разберёмся: что такое псевдослучайные числа, чем они отличаются от случайных, зачем вообще нужны и где применяются.
Начнём с понятия случайных чисел, которые правильней считать истинно случайными числами. Это некие непредсказуемые значения, которые на сегодняшний момент невозможно умышленно воспроизвести.
Учёные научились добывать истинно случайные числа из физических процессов окружающего мира с помощью аппаратных генераторов. Одно из первых подобных устройств появилось в 1957 году и называлось ERNIE.
Это был аппарат со стеклянными трубками, заполненными неоном. Под действием высокого напряжения электроны внутри трубок отрывались от атомов неона, хаотично двигались и создавали случайный шум. Компьютер усиливал этот шум и преобразовывал полученные данные в случайные числа.
Видео: Rod Willerton
Современные способы генерации истинно случайных чисел стали более технологичными и менее громоздкими. Например, британские инженеры научились использовать кристаллическую решётку химических растворов.
Для этого они заливают в ёмкость жидкий раствор и направляют на него камеру для фиксации хаотично формирующихся кристаллов. Сделанные фотографии анализирует алгоритм, который переводит кристаллические узоры в бинарный код. Затем этот код преобразуется в случайные числа.
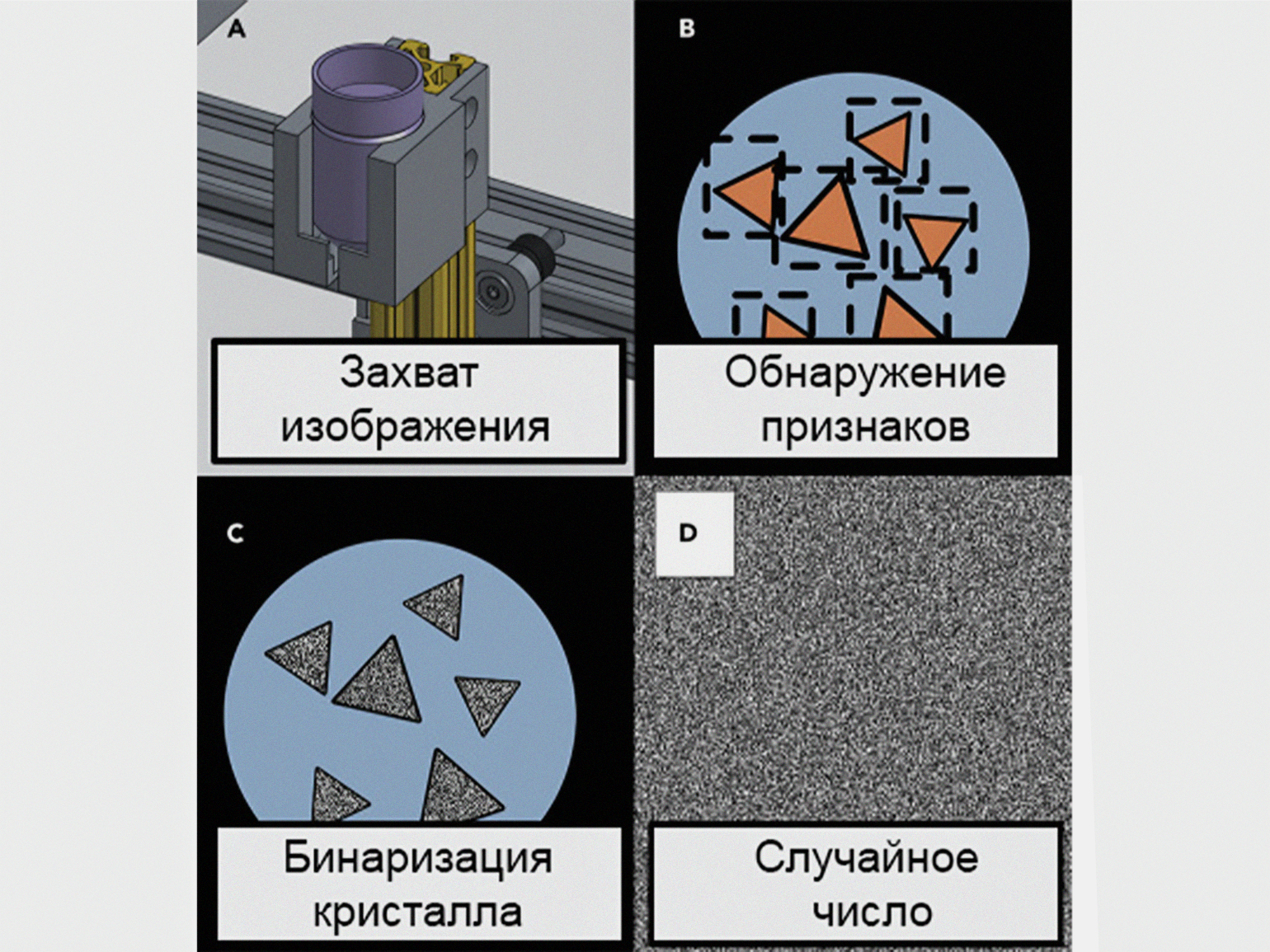
Изображение: University of Glasgow / Cell Press
У аппаратных генераторов истинно случайных чисел есть ограничения по скорости работы и количеству выдаваемых чисел в заданном диапазоне. Также многие из них дороги в обслуживании и склонны к деградации. Например, если аппарат построен на основе радиоактивного вещества, то со временем его количество может снизиться и это приведёт к погрешностям.
Учёным нужно было работать со случайными числами и придумать способ нивелировать недостатки аппаратных генераторов истинно случайных чисел. Так появились генераторы псевдослучайных чисел, которые вместо физических процессов используют детерминированный алгоритм — рассчитывают случайные числа на основе математических формул.
Ниже цитата профессора Мадса Хаара, основателя Random.org — генератора истинно случайных чисел с помощью атмосферного шума:
«Генераторы псевдослучайных чисел (ГПСЧ) эффективны, то есть могут создавать множество чисел за короткое время, и детерминированы, что означает, что заданная последовательность чисел может быть воспроизведена позже, если известна начальная точка последовательности.
Эффективность — хорошая характеристика, если вашему приложению требуется много чисел, а детерминизм удобен, если вам нужно снова воспроизвести ту же последовательность чисел на более позднем этапе. ГПСЧ обычно также являются периодическими, что означает, что последовательность в конечном итоге будет повторяться. Хотя периодичность вряд ли когда-либо является желательной характеристикой, современные ГПСЧ имеют период, который настолько велик, что его можно игнорировать для большинства практических целей.
Эти характеристики делают ГПСЧ подходящими для приложений, где требуется много чисел и где полезно легко воспроизводить одну и ту же последовательность. Популярными примерами таких приложений являются моделирование и симуляции.
ГПСЧ не подходят для приложений, где важно, чтобы числа были действительно непредсказуемыми, например для шифрования данных и азартных игр».
Профессор Мадс Хаар,
основатель Random.org, доцент факультета компьютерных наук и статистики в Дублине
Сейчас генераторы псевдослучайных чисел встроены во многие языки программирования. В Python за это отвечает модуль random. В следующих разделах мы разберём принцип работы модуля и его основные функции.
Случайные и псевдослучайные числа используются во многих сферах, где важна непредсказуемость. Например, при регистрации на новом сайте современные браузеры предложат вам пароль из случайных символов. В этом случае непредсказуемость повышает безопасность учётной записи.
Подобные примеры встречаются в машинном обучении, тестировании, маркетинге, разработке игр и других областях. Ниже мы добавим статьи о различных направлениях, в которых не обходится без случайных чисел:
- «Уравниваем шансы: как работает случайность в играх»;
- «Что такое рекомендательные системы и как они работают»;
- «SSH: что это и как им пользоваться — гайд для новичков»;
- «Беспарольная аутентификация: что это такое и почему на неё делают ставку IT-гиганты»;
- «Что такое QA-тестирование и как оно устроено»;
- «Что такое пентесты и для чего они нужны»;
- «Как устроено машинное обучение: задачи, алгоритмы и виды machine learning»;
- «Что такое нейросеть и как она работает»;
- «Как понять, что продавать на Wildberries? Понятная инструкция по анализу ниши»;
- «SWOT-анализ: что это такое и как его провести. Разбираем на примерах из России».
Для закрепления материала рекомендуем посмотреть фрагмент лекции о предназначении библиотеки random в разных языках программирования:
Видео: «Vanechki: математика, биология и многое другое»
Как работает генерация случайных чисел в Python
Для получения псевдослучайных чисел Python использует алгоритм «Вихрь Мерсенна». Для понимания его работы представьте вращающийся вихрь, заполненный числами. Когда вы используете функции модуля random, алгоритм выхватывает из вихря несколько чисел и создаёт на их основе случайное число. Это случайное число выводится в консоль, а взятые из вихря числа возвращаются, и процесс может повторяться множество раз.
«Вихрь Мерсенна» работает быстро и позволяет сгенерировать большое количество случайных чисел до момента, когда они начнут повторяться. После запуска алгоритм обрабатывает начальное значение (seed), которое в Python можно задать вручную или оставить со значением по умолчанию.
Если вы укажете начальное значение вручную, то при каждом запуске алгоритм будет генерить одинаковую последовательность чисел. Это может быть полезно для отладки или тестирования приложения, когда нужно много раз воспроизвести код и оценить результаты его работы.
По умолчанию начальное значение явно не указано, и за его основу Python берёт текущее время в операционной системе. Это позволяет при каждом запуске программы видеть новую последовательность случайных чисел.
В этом разделе мы сильно упростили принцип получения случайных чисел из «Вихря Мерсенна». Если вам интересны технические подробности — рекомендуем статью The Mersenne Twister инженера Джона Саварда.

Изображение: Joe Saward / Quadibloc

Читайте также:
Функции модуля random
Модуль random входит в стандартную библиотеку Python и относится к числовым и математическим модулям. В этом разделе мы расскажем об основных функциях и для удобства разделим их на группы по назначению.
Перед знакомством с функциями вам нужно установить Python под свою ОС, создать в редакторе файл с расширением .py и импортировать модуль библиотеки random. Импорт записывается одной строкой в начале файла:
import random
# Модуль random подключён, и теперь можно писать функции. Функции для генерации случайных чисел в диапазоне
Представленные в этом разделе функции возвращают целые числа или числа с плавающей точкой в определённом диапазоне. Этот диапазон может задаваться параметрами функции или выставляться вручную.
Для выбора случайных чисел все функции используют непрерывное равномерное распределение. Это означает, что все числа в диапазоне могут выпасть с одинаковой вероятностью.
Видео: «Матан»
random.random(): возвращает число с плавающей точкой в диапазоне 0.0 <= N < 1.0
Функция random() возвращает случайно сгенерированное число начиная с нуля и заканчивая единицей. Ноль может вернуться, а единица нет. Единица в данной функции находится за пределами числового диапазона.
import random
print(random.random())
Примеры результатов:
- 0.0971227764408;
- 0.458461556054;
- 0.333821679312;
- 0.511654197738;
- 0.774338286083.
random.uniform(a, b): возвращает число с плавающей точкой в диапазоне a <= N <= b
Для функции uniform() вы должны вручную выставить диапазон для генерации случайного числа. Функция вернёт число с плавающей точкой, которое может равняться начальной или конечной границе диапазона.
import random
print(random.uniform(2.5, 5.5))
Примеры результатов:
- 3.98864976695;
- 4.16381651811;
- 5.19473678325;
- 4.67089126496;
- 3.04033733076.
Для указания границ диапазона можно использовать целые числа. Однако функция uniform() всё равно будет возвращать число с плавающей точкой.
import random
print(random.uniform(2, 5))
Примеры результатов:
- 2.18071074823;
- 4.12138593074;
- 4.42796643605;
- 2.87651870385;
- 2.31154629523.
random.randint(a, b): возвращает целое число в диапазоне
a <= N <= b
Для функции randint() вы вручную задаёте диапазон, и из него в консоль выводится случайное целое число. Границы диапазона учитываются.
import random
print(random.randint(1, 10))
Примеры результатов:
- 9;
- 3;
- 8;
- 7;
- 1.
random.randrange(start, stop, step): возвращает целое число в заданном диапазоне с учётом шага
Для функции randrange() вам нужно обязательно указать два аргумента: начальное и конечное значение числового диапазона. После в консоль попадёт случайное целое число, которое может совпадать с начальным значением диапазона. Конечное значение диапазона выпасть не может.
Третий аргумент необязательный. Он отвечает за шаг, с которым функция randrange() будет перебирать последовательность чисел в заданном диапазоне. Если шаг не указан, то его значение будет равняться единице.
Функция randrange() с шагом по умолчанию:
import random
print(random.randrange(1, 20))
Примеры результатов:
- 5;
- 1;
- 1;
- 5;
- 4.
Функция randrange() с шагом 4:
import random
print(random.randrange(1, 20, 4))
Примеры результатов:
- 13;
- 5;
- 9;
- 17;
- 17.
Функции для работы с коллекциями
Коллекции — это общий термин, которым в языке Python обозначают сгруппированные наборы данных. Если эти данные упорядочены, то они называются последовательностями. К последовательностям можно отнести любые итерируемые объекты, которые можно перебрать по одному элементу за раз. Это списки, строки, кортежи и другие данные. В документации для обозначения последовательностей используется сокращение seq — это от слова sequence, «последовательность».
Если данные хранятся хаотично, то их считают неупорядоченными коллекциями. В документации они обозначены словом population. К примерам неупорядоченных коллекций относятся множества и словари.
Если вы до этого не работали с коллекциями — рекомендуем перед дальнейшей работой с модулем random посмотреть следующие статьи:
Для удобства мы будем применять модуль random для числового списка.
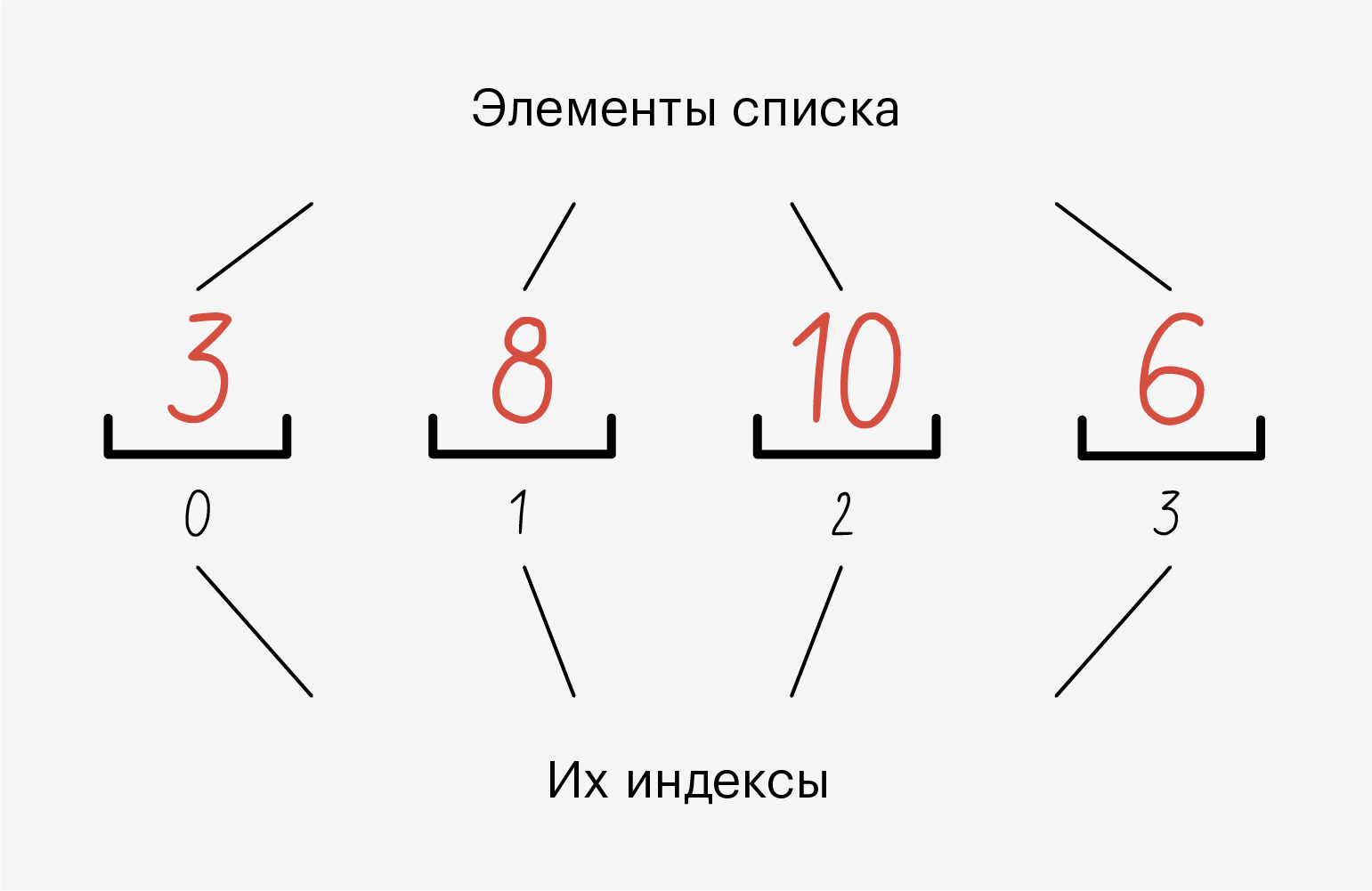
Иллюстрация: Оля Ежак для Skillbox Media
random.choice(seq): возвращает случайный элемент из последовательности
Функция choice() нужна для выбора одного элемента из заполненной последовательности. В выборке участвуют все без исключения элементы.
Однако если вызвать функцию choice() и в качестве аргумента передать ей пустую последовательность, то в консоли высветится ошибка IndexError.
import random
print(random.choice([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]))
Примеры результатов:
- 2;
- 9;
- 1;
- 3;
- 3.
random.sample(population, k): выбирает случайные элементы из коллекции
Функция sample() работает для последовательностей и неупорядоченных коллекций вроде множества. Для этой функции первым аргументом вы передаёте коллекцию, а вторым — количество уникальных элементов, которые нужно выбрать из этой коллекции. Пример: в коллекции десять элементов и вы хотите выбрать пять. В этом случае при каждом запуске функция sample() будет выводить в консоль пять уникальных элементов.
Однако вы получите ошибку, если количество уникальных элементов будет больше размера коллекции. То есть в коллекции десять элементов, а вы захотите увидеть в консоли пятнадцать. Так эта функция не работает.
import random
print(random.sample([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], 5))
Примеры результатов:
- [5, 6, 10, 7, 1];
- [2, 3, 4, 10, 8];
- [6, 8, 2, 1, 5];
- [3, 5, 8, 4, 7];
- [8, 10, 3, 9, 5].
Если вам нужно, чтобы элементы из последовательности повторялись, то для этого подойдёт функция random.choices(). По принципу работы она похожа на random.sample(), но обладает гибкими настройками для выбора случайных элементов. Подробно об этих настройках можно узнать из документации.
random.shuffle(seq): в случайном порядке перемешивает последовательность элементов
Для запуска функции shuffle() вам необходимо предварительно создать переменную, добавить в неё последовательность, затем вызвать функцию и вывести результат в консоль. Если вы попробуете сразу вызывать функцию и напечатать результат в консоль, то получите значение None.
import random
numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
random.shuffle(numbers)
print(numbers)
Примеры результатов:
- [3, 7, 2, 4, 1, 8, 5, 6, 10, 9];
- [2, 1, 5, 4, 6, 3, 10, 9, 7, 8];
- [7, 8, 9, 5, 10, 2, 3, 1, 4, 6];
- [6, 10, 8, 1, 4, 3, 9, 7, 2, 5];
- [5, 10, 7, 9, 4, 8, 2, 6, 1, 3].
При каждом вызове функция shuffle() не только перемешивает элементы, но и сохраняет их новое расположение в переменную. Если вам важно после перемешивания сохранить исходное расположение элементов, то для этого нужно создать ещё одну переменную с копией нужного списка.
import random
original_list = [1, 2, 3, 4, 5]
shuffled_list = original_list[:]
random.shuffle(shuffled_list)
print("Original list:", original_list)
print("Shuffled list:", shuffled_list)Пример результата:
- («Original list:», [1, 2, 3, 4, 5]);
- («Shuffled list:», [3, 1, 4, 5, 2]).
Функции для методов распределения
Под распределением в теории вероятностей понимают закон, по которому одна величина соответствует другой. Установить соответствие между величинами можно разными способами за счёт методов распределения. Например, если мы будем бросать кубик, то методы распределения помогут определить вероятность выпадения чисел в диапазоне от 1 до 6.
Методов распределения много, и далее мы рассмотрим функции модуля random для основных из них. Остальные методы более специфичны, и их описание вы найдёте в документации.
Если вы только знакомитесь с распределением, рекомендуем сначала прочесть следующие статьи:
normalvariate(mu, sigma): выдаёт случайное число по закону нормального распределения
Метод нормального распределения используется для проверки гипотез, когда для статистического анализа собрана большая выборка данных. Визуально этот тип распределения напоминает симметричный колокол, принцип работы которого наглядно продемонстрирован на доске Гальтона.
Видео: Sciencelab
Видео: «Прикладная статистика»
Для генерации случайного числа функции normalvariate() нужно передать два параметра. Первый параметр mu — отвечает за среднее значение распределения. Второй параметр sigma — стандартное отклонение. В примере ниже мы берём среднее значение 0 и стандартное отклонение 1.
import random
mu = 0
sigma = 1
random_number = random.normalvariate(mu, sigma)
print(random_number)Примеры результатов:
- −1.04069136656;
- 1.56106418963;
- 2.15752839674;
- −0.00216864768154;
- 0.157904318103.
Если использовать функцию normalvariate() вместе с циклами, то можно получить сразу несколько чисел, распределённых по нормальному закону.
import random
mu = 0
sigma = 1
random_numbers = [random.normalvariate(mu, sigma) for _ in range(10)]
print(random_numbers)Пример результата из десяти случайных чисел:
0.24299953033900287, 0.5537962330705753, 1.9218644750764622, −1.2106188146738326, −1.609069662113085, 2.3850359922986226, −0.19805893931375596, −0.1076120346364513, 0.3939314031552044, 0.7194200521076376.
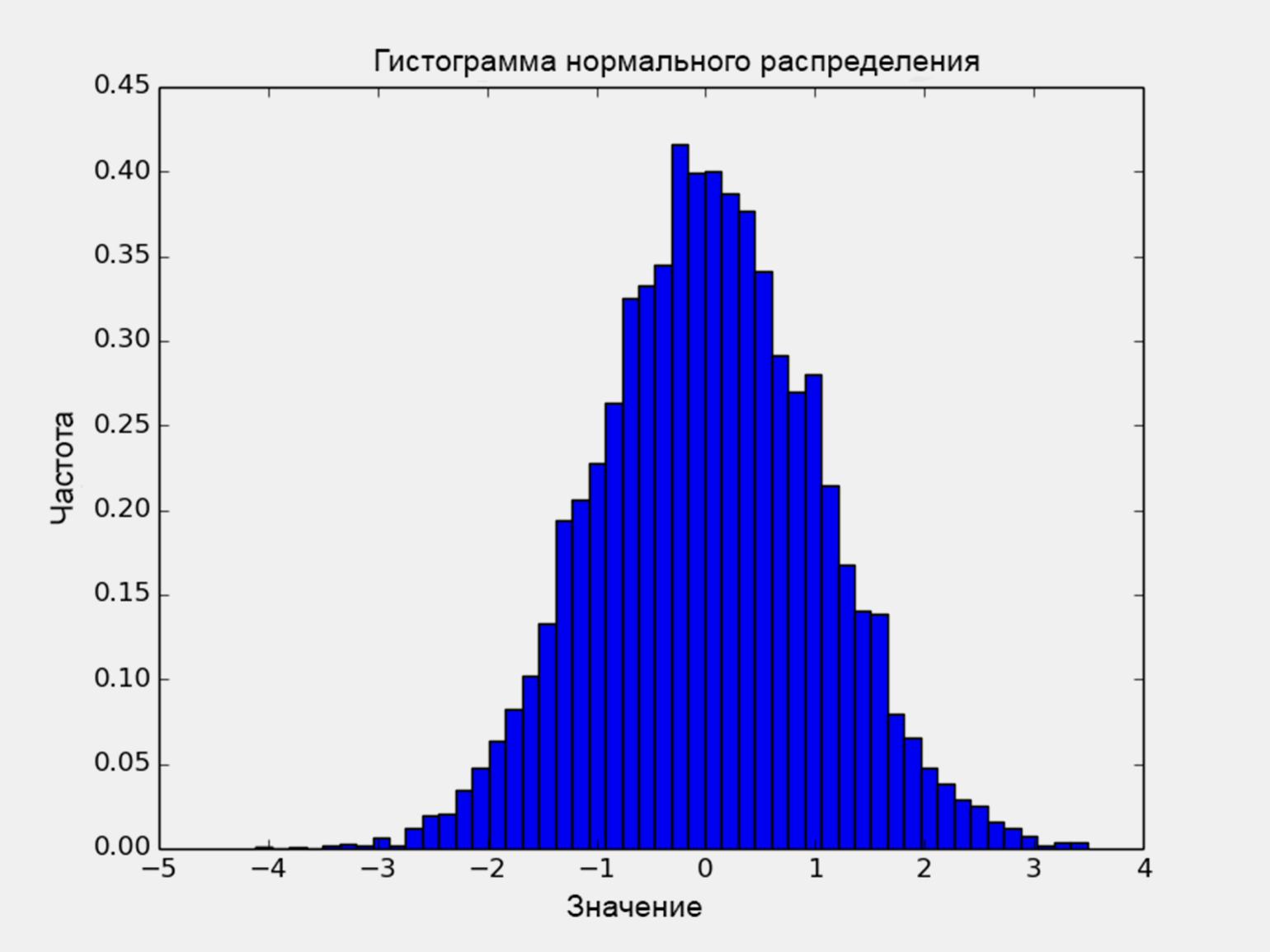
Для удобства вы можете подключить библиотеку Matplotlib и наблюдать за визуальным распределением случайных чисел с помощью графиков. Чем больший числовой диапазон вы укажете, тем наглядней будет картинка.
import random
import matplotlib.pyplot as plt
mu = 0
sigma = 1
random_numbers = [random.normalvariate(mu, sigma) for _ in range(10000)]
plt.hist(random_numbers, bins=50, density=True)
plt.title("Histogram of normal distribution")
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.show()Пример гистограммы для 10 000 случайно сгенерированных чисел:
lognormalvariate(mu, sigma): создаёт случайные числа по закону логнормального распределения
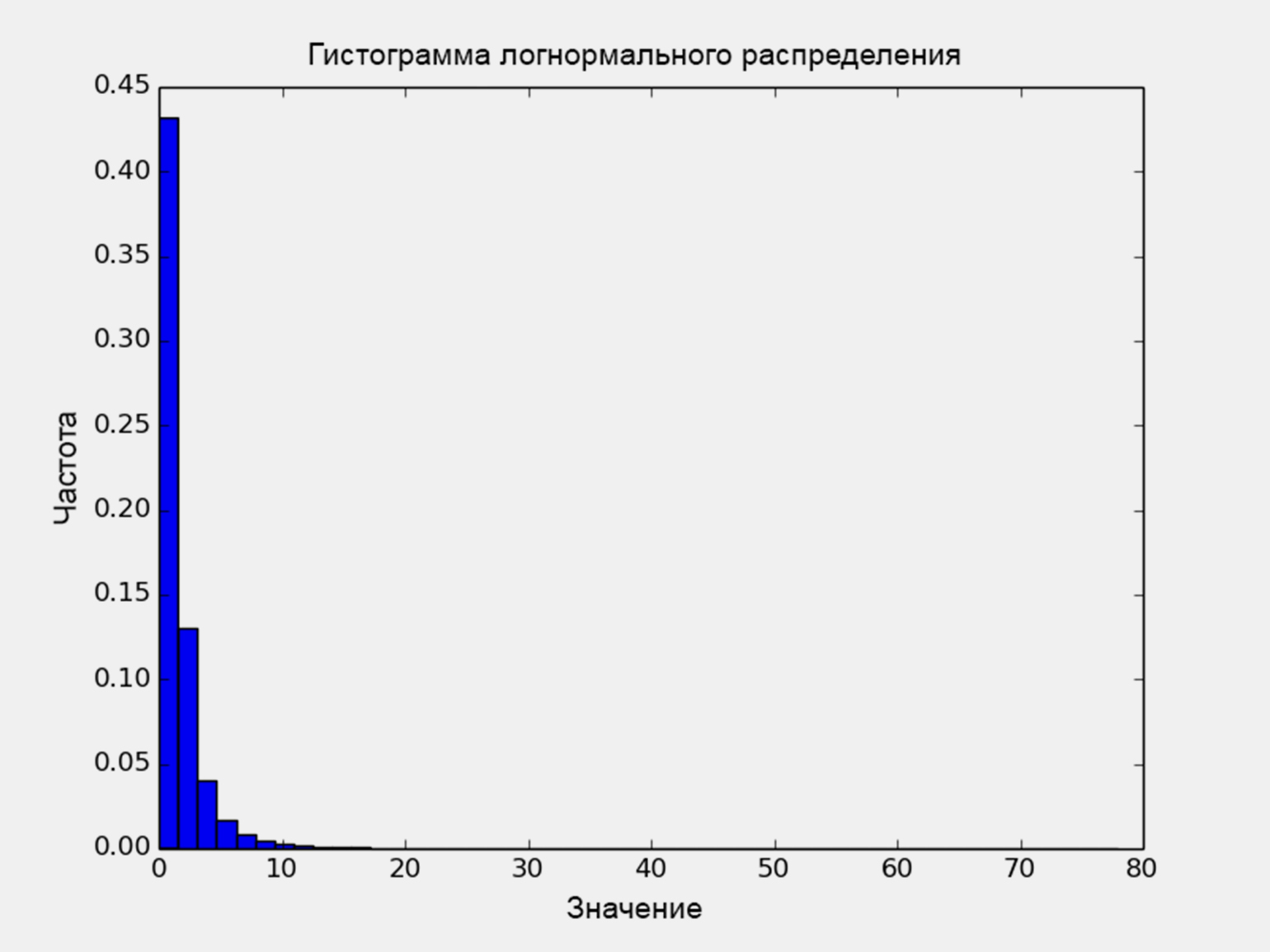
Метод логнормального распределения предназначен для моделирования данных, которые изменяются экспоненциально. Например, в финансовой сфере такое распределение помогает смоделировать колебание цен на акции, ведь у них нет фиксированного значения для роста или снижения.
Видео: Борис Бояршинов
Для работы функции lognormalvariate(mu, sigma) нужны те же параметры, которые мы использовали для настройки нормального распределения: нужно указать mu для среднего значения распределения и sigma — для определения стандартного отклонения. Также мы можем добавлять циклы и подключить библиотеку Matplotlib для визуализации полученных данных.
import random
import matplotlib.pyplot as plt
mu = 0
sigma = 1
random_numbers = [random.lognormvariate(mu, sigma) for _ in range(10000)]
plt.hist(random_numbers, bins=50, density=True)
plt.title("Histogram of lognormal distribution")
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.show()Пример гистограммы логнормального распределения, которая получена для 10 000 случайно сгенерированных чисел:
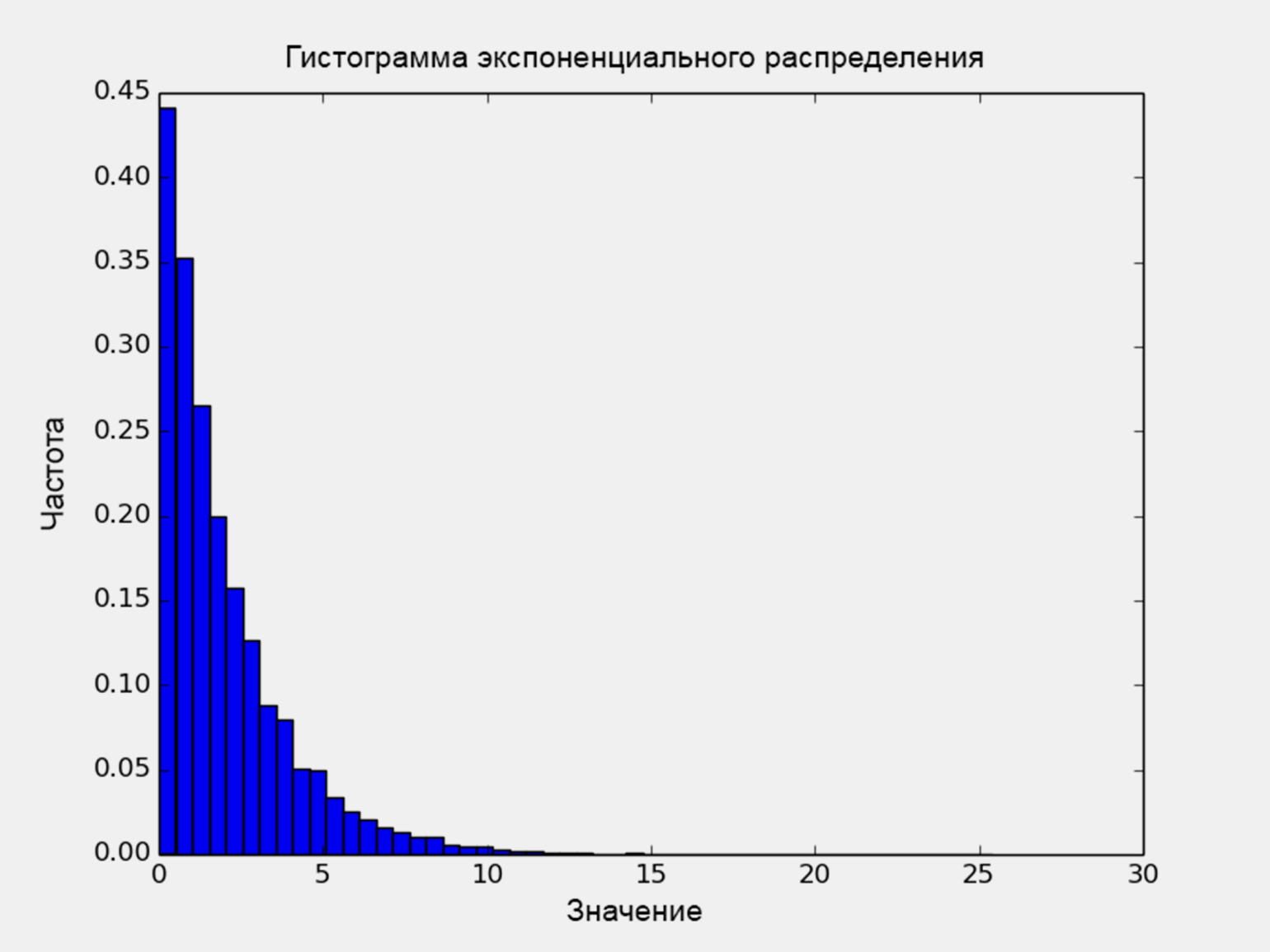
random.expovariate(lambd): генерит случайные числа по закону экспоненциального распределения
Метод экспоненциального распределения полезен для моделирования временных интервалов между последовательными и независимыми событиями, которые происходят со стационарной интенсивностью. Вот представьте, что вы получили сообщение. Теперь новое сообщение вы можете получить в любое время — момент получения предыдущего сообщения на это не влияет. Это и будет стационарной интенсивностью.
Видео: «Прикладная статистика»
Как и в случае с предыдущими методами распределения, функция expovariate () совместима с циклами и библиотекой Matplotlib. Однако в качестве параметра нужно передавать lamd — интенсивность событий.
import random
import matplotlib.pyplot as plt
lambd = 0.5
random_numbers = [random.expovariate(lambd) for _ in range(10000)]
plt.hist(random_numbers, bins=50, density=True)
plt.title("Histogram of exponential distribution")
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.show()Пример гистограммы экспоненциального распределения для 10 000 случайно сгенерированных чисел:
Проекты с модулем random
В этом разделе мы будем получать случайные значения на практике. Рекомендуем выполнить несколько проектов, чтобы закрепить теорию.
Игра «Змейка» на Pygame
Для реализации проекта вам понадобятся библиотеки Pygame и random. Вы создадите игровое поле, добавите еду, научите змейку двигаться и увеличиваться в размерах — в общем полностью напишете игру с нуля.
Читайте также:
Игра «Угадай число»
Для этого проекта вам понадобится только библиотека random. Вы научите программу загадывать случайное число и попробуете его угадать. Если совершите неудачную попытку — программа подскажет, каким должно быть правильное число: больше или меньше указанного. Если угадаете — получите поздравление и узнаете, сколько попыток пришлось потратить.
Генератор случайных аватарок на Pillow
В этом проекте вы подключите библиотеку Pillow и создадите небольшие пиксельные изображения (5×5), как на дефолтных аватарках с сайта GitHub.

Изображение: Jason Long / GitHub
Затем вы сможете раскрасить полученные пиксельные изображения случайными цветами, которые поможет выбрать модуль random. Цвета будут определяться случайно, но с ограничением по оттенку — не должны быть слишком тёмными. Ещё можно будет добавить рамку вокруг аватара.

Читайте также:
Что дальше
Помимо модуля random, в Python есть и другие инструменты, которые упрощают проведение математических операций. О возможностях некоторых из таких инструментов мы рассказали в отдельных статьях:
- «Библиотека NumPy: всё, что нужно знать новичку». Это библиотека для работы с многомерными массивами, которую программисты часто используют для анализа данных и обучения нейронных сетей.
- «Округление в Python: выбираем лучший способ». Чтобы превратить десятичную дробь в целое число можно использовать стандартные функции round() и int() или подключить модули math и decimal.
- «Библиотека Scikit-learn: как создать свой первый ML‑проект». Это библиотека с набором основных алгоритмов машинного обучения: регрессией, классификацией, кластеризацией и другими методами.
- «Работаем с Pandas: основные понятия и реальные данные». Pandas поддерживает основные статистические методы для работы с данными, полезна при подготовке первичного анализа и аналитики.
- «Библиотека Matplotlib для построения графиков». Это библиотека для построения графиков и визуализации данных. Позволяет создавать линейные и круговые диаграммы, гистограммы и много что ещё.
А если вам нужно генерировать случайные числа для криптографических целей, то для этого в Python предусмотрен модуль secrets. Он позволяет создавать криптостойкие случайные числа, для которых характерен высокий уровень безопасности. На основе этого модуля можно создавать пароли, цифровые токены и данные для аутентификации в учётной записи.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!
Python для всех
Вы освоите Python на практике и создадите проекты для портфолио — телеграм-бот, веб-парсер и сайт с нуля. А ещё получите готовый план выхода на удалёнку и фриланс. Спикер — руководитель отдела разработки в «Сбере».
Пройти бесплатно



