Что такое энтропия: объясняем простыми словами с примерами из физики и жизни
Из-за неё время не отмотать назад, а Вселенную ждёт тепловая смерть.

Наша редакция любит не только программирование, но и науку — особенно когда концепции помогают лучше понимать технологии. Сегодня поговорим об энтропии. Этот термин напрямую связан с криптографией, сжатием данных, машинным обучением и тем, как IT-системы деградируют со временем. Понимание энтропии даёт глубокий взгляд на процессы, с которыми вы работаете каждый день, — от генерации случайных чисел до оптимизации баз данных.
Мы постараемся объяснить всё простыми словами и рассмотрим термин с разных сторон: что такое энтропия как универсальная мера беспорядка, как она проявляется в термодинамике, как используется в информатике и почему объясняет необратимость времени и его направление. Считайте это вводной статьёй для новичков — после неё вам будет проще разбираться в более сложных материалах по физике, теории информации и их применению в технологиях.
Содержание
- Что такое энтропия и как её понимать
- Энтропия в термодинамике: как всё началось
- Энтропия в информатике и теории информации
- Как энтропия объясняет движение времени
Что такое энтропия и как её понимать
Энтропия — это физическая величина, связанная с количеством микросостояний системы. Микросостояния — это способы расположения частиц на атомном уровне, которые соответствуют одному и тому же наблюдаемому макросостоянию. Чем больше микросостояний, тем выше энтропия. Понимаем, звучит достаточно сложно, поэтому разберём на примере обычной фарфоровой чашки.
Для простоты возьмём два макросостояния: «чашка целая» и «чашка разбитая». Когда чашка целая, её структура упорядочена — атомы и связи расположены примерно «как надо», с небольшими тепловыми колебаниями и микровариациями. Таких микросостояний много, однако по сравнению с разбитой чашкой их относительно немного. Это состояние с низкой энтропией.
Если уронить чашку, она разлетится. Но как именно? Она может расколоться на две части, на три или на тысячи осколков. Осколки могут оказаться где угодно — под столом, у двери, в противоположных углах комнаты. Способов, как может выглядеть «разбитая чашка», колоссально больше. В популярных объяснениях это называют ростом «беспорядка». Это и есть состояние с высокой энтропией.
Здесь важно уточнить: дело не в том, что «природа стремится к хаосу». В изолированных системах (или когда обмен энергией и веществом с окружением минимален) система почти всегда переходит из менее вероятных состояний в более вероятные. Более вероятны именно те состояния, которым соответствует гораздо больше микросостояний. Поэтому переход «целое → разбито» статистически естественен, а обратный переход («разбито → целое») настолько маловероятен, что ждать его бессмысленно: разбитая чашка сама не соберётся.

Энтропия в термодинамике: как всё началось
Понимание энтропии появилось не из каких-то абстрактных размышлений, а из вполне конкретных задач промышленной революции. Дальше мы разберём, как энтропия возникла в контексте тепловых машин, что именно она означала в формулировке Клаузиуса и как физика Больцмана связала её с микросостояниями.
От паровых машин к идее перепада температур
В конце XVIII — начале XIX века термодинамика развивалась во многом благодаря попыткам повысить эффективность тепловых машин, особенно паровых двигателей, которые приводили в движение фабрики, насосы и железнодорожные локомотивы. Эти машины обладали низким КПД — всего 2–5%. Из-за этого они сжигали огромное количество угля, но получали минимум полезной работы.
В 1824 году французский инженер Сади Карно опубликовал работу «Размышления о движущей силе огня и о машинах, способных развивать эту силу». Он абстрагировался от деталей конкретных машин и рассуждал в общем виде: как водяная мельница получает работу благодаря перепаду высот воды, так и тепловая машина получает работу за счёт перепада температур — когда тепло переходит от горячего тела к холодному. Это привело его к мысли, что превратить всё полученное тепло в механическую работу на 100% принципиально невозможно: даже в идеальной машине не обойтись без трения и потерь.
Часть энергии неизбежно переходит в менее упорядоченную форму — рассеивается в окружающую среду в виде тепла с более низкой температурой. По мере того как температуры выравниваются, способность системы совершать полезную работу уменьшается. При этом общее количество энергии в системе остаётся неизменным согласно закону сохранения энергии: энергия не исчезает, она просто становится менее доступной для извлечения работы.
Для большей ясности попробуйте вообразить водопад: пока существует перепад высот, вода может крутить колесо мельницы и совершать полезную работу. Но когда река выровняется и станет спокойной, никакой работы из неё не получишь — хотя воды в ней столько же и её полная энергия не изменилась. Так и с теплом: пока есть горячее и холодное тело — существует температурный перепад, и можно получать работу. А когда температуры выровнялись — остаётся только равномерно рассеянное тепло, из которого работу извлечь уже невозможно.
Как возникло современное понимание энтропии
В 1865 году физик Рудольф Клаузиус ввёл термин «энтропия» и строго связал его со вторым началом термодинамики. Если совсем просто: энтропия показывает, насколько энергия «размазана» по системе и насколько трудно повернуть процесс вспять. Чем выше энтропия, тем меньше «запаса упорядоченности», из которого можно извлечь полезную работу. Именно поэтому процессы в природе необратимы: в изолированной системе энтропия не может самопроизвольно уменьшаться — она может либо оставаться постоянной, либо возрастать.
Дальше возник естественный вопрос: почему второе начало термодинамики вообще работает, если на микроскопическом уровне законы физики обратимы во времени? Ведь уравнения движения частиц симметричны: если «прокрутить» столкновение назад, оно останется физически допустимым. Прояснить этот парадокс помогла статистическая физика, прежде всего работы австрийского физика Людвига Больцмана во второй половине XIX века.
Больцман установил связь между термодинамической энтропией и числом возможных микросостояний системы (обозначается W):
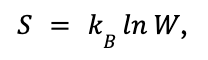
где kB — постоянная Больцмана (примерно 1,38 × 10⁻²³ Дж/К).
Суть в следующем: одно и то же наблюдаемое макросостояние (например, когда газ занимает весь объём помещения) может быть реализовано через огромное число различных микросостояний — конкретных комбинаций положений и скоростей всех частиц. Система при своей эволюции почти всегда переходит к тем макросостояниям, которым соответствует статистически больше микросостояний, — просто потому, что вероятность оказаться в таком состоянии выше.
Больцман попытался объяснить это с точки зрения вероятности и статистики. Его ключевая идея звучит примерно так: состояние «температуры выровнялись» соответствует гораздо большему числу микросостояний, чем состояние «всё строго разделено на горячее и холодное». Например, если в системе миллиард частиц, то конфигураций с примерно равномерным распределением энергии по всем частицам существует астрономически больше, чем конфигураций, где все быстрые частицы в одной половине объёма, а все медленные — в другой. Поэтому выравнивание температур статистически вероятнее: система просто «блуждает» по своим микросостояниям и почти неизбежно попадает в те, которых больше.
Давайте ненадолго абстрагируемся от формул и представим коробку с песком: снизу слой чёрного, сверху — слой белого. Это сильно упорядоченное состояние с низкой энтропией. Если встряхнуть коробку, песок перемещается и станет серым — энтропия возрастёт. Теоретически песчинки могли бы случайно снова разойтись по слоям и вернуться к исходному состоянию. Но на практике у перемешанного состояния существует астрономически больше микровариантов расположения песчинок, чем у аккуратного разделения на два слоя.
Поэтому при встряхиваниях происходит смешивание, а не разделение. В этом статистическом смысле энтропия растёт — не потому, что энергия или частицы «теряются», а потому, что система переходит в более вероятные состояния.

Изображение: Skillbox Media
Энтропия в информатике и теории информации
В середине XX века понятие энтропии перешло из физики в информатику. Всё началось с практической проблемы: инженеры AT& T работали с дорогими телефонными линиями, где сигнал затухал, а при усилении вместе с голосом усиливался шум. Нужно было понять, сколько информации можно передать через канал связи и как сделать это с минимумом искажений.
Одним из ведущих исследователей в Bell Labs был Клод Шеннон — будущий «отец теории информации». В своей статье «Математическая теория связи» он впервые определил понятие информационной энтропии как меру неопределённости или непредсказуемости источника сообщений и вывел для неё такую формулу:
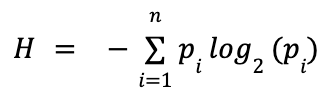
- H — энтропия, то есть средняя неопределённость на один символ (измеряется в битах);
- pi — вероятность появления i-го символа;
- log2 — логарифм по основанию 2 (переводит результат в биты).
Предположим, вы загадываете букву из набора, в котором есть только одна буква — «А». В этом случае неопределённости нет, поскольку исход известен заранее, и энтропия равна нулю. Но если вы выбираете букву случайным образом из всего русского алфавита (33 буквы), то вариантов становится больше, и энтропия растёт — необходимо больше информации, чтобы угадать, какую букву вы задумали.
Клод Шеннон использовал энтропию для анализа передачи данных по каналам связи. Однако идея оказалась достаточно универсальной и нашла применение в других областях — например, в криптографии для оценки стойкости паролей.
Чтобы оценить стойкость пароля, воспользуемся упрощённой формулой Хартли:
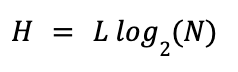
- H — энтропия пароля в битах;
- L — длина пароля;
- N — мощность алфавита (число различных символов);
- log2(N) — «вес» одного символа в битах.
Для закрепления сравним три пароля и попробуем определить, какой из них наиболее защищён: 2580, Cat! 5 и correct horse battery staple.
| 2580 | Cat!5 |
correct horse battery staple |
|
|---|---|---|---|
| Модель оценки | Случайные символы (Хартли) | Случайные символы (Хартли) | Случайные слова из списка |
| Длина (L) | 4 символа | 5 символов | 4 символа |
| Алфавит / словарь | Цифры 0–9 | Печатные ASCII-символы | Список из ~2048 слов |
| Мощность (N) | 10 | 95 | 2048 |
| «Вес» элемента | log₂(10) ≈ 3,32 бита/символ | log₂(95) ≈ 6,57 бита/символа | log₂(2048) = 11 бит/слово |
| Энтропия (≈) | 4 × 3,32 ≈ 13,3 бита | 5 × 6,57 ≈ 32,8 бита | 4 × 11 = 44 бита |
| Комбинаций (≈) | 10 000 | ≈ 8,5 млрд | 2^44 |
Хотя пароль Cat! 5 использует широкий алфавит, фраза вроде correct horse battery staple часто надёжнее за счёт длины в словах, если слова выбраны случайно.
Однако важно отметить, что формула Хартли работает только для случайно выбранных символов. Например, пароль P@ssword1 содержит заглавные буквы, спецсимволы и цифры, но его реальная стойкость намного ниже расчётной: люди используют предсказуемые шаблоны и замены вроде a→@ или o→0. Хакеры это знают — они применяют словарные атаки и «маски», которые резко сокращают число вариантов для перебора. То есть длинная случайная фраза из простых слов чаще надёжнее короткого «сложного» пароля с предсказуемыми заменами.

Читайте также:
Как энтропия объясняет движение времени
В конце 1920-х астрофизик Артур Эддингтон популяризировал термин «стрела времени», связав наблюдаемое направление течения времени с ростом энтропии. Его идея в том, что мы почти всегда наблюдаем процессы, которые развиваются в одном направлении — от прошлого к будущему. Эта односторонность объясняется фундаментальным принципом: энтропия изолированных систем не убывает со временем — она либо остаётся постоянной, либо возрастает.
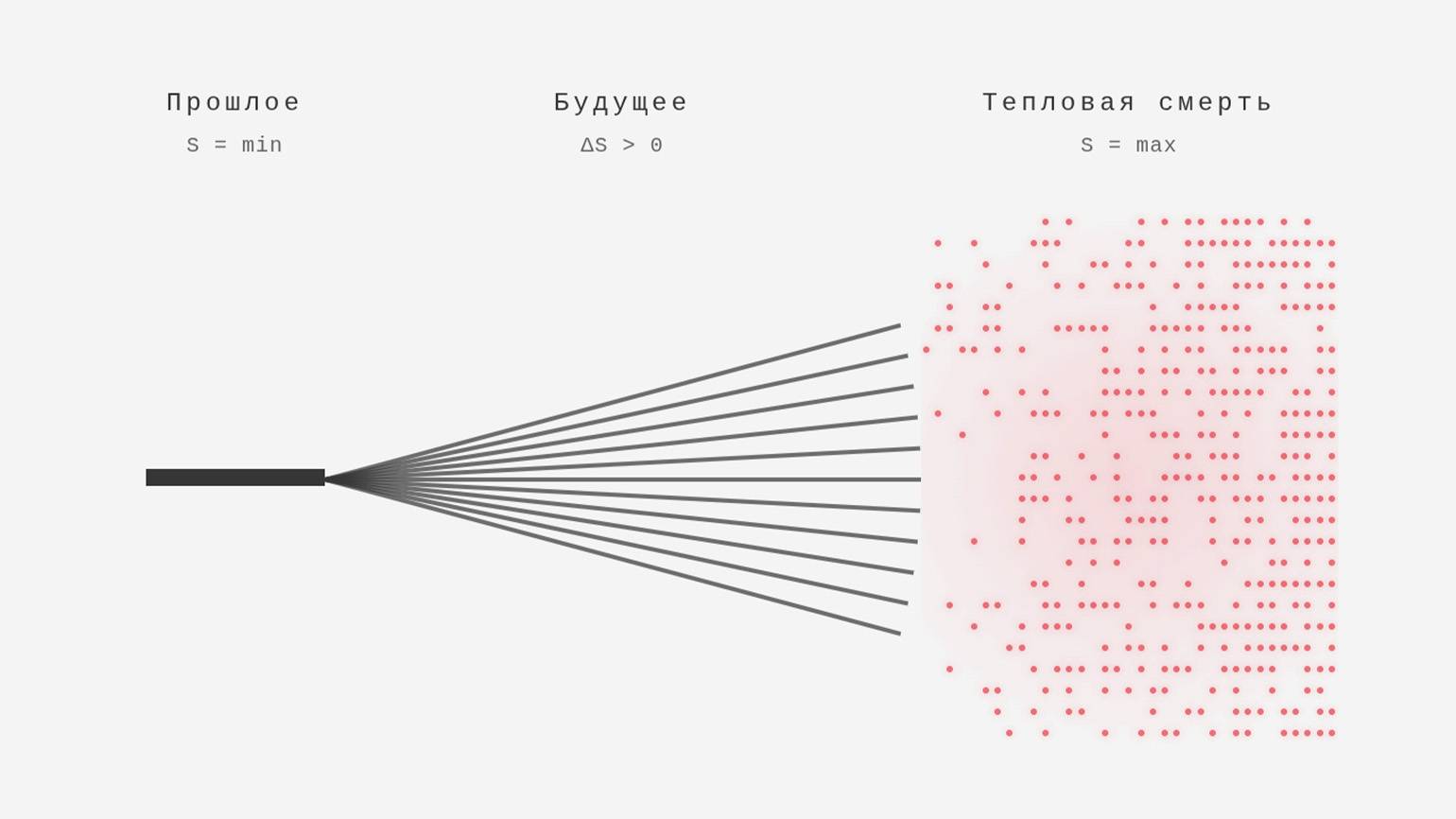
Представьте время как дерево решений для наблюдателя. Прошлое похоже на ствол: оно зафиксировано, событие произошло, и остался лишь один факт. А вот будущее напоминает ветви: оно ещё не случилось, поэтому описывается множеством возможных сценариев. На каждом шаге возникают развилки, и чем дальше вперёд, тем больше возможных вариантов. Поэтому мы ощущаем течение времени как переход от «одного случившегося» ко «множеству возможных».
На языке физики это объясняется тем, что макроскопические системы почти всегда эволюционируют к более вероятным состояниям — тем, которым соответствует больше микросостояний. Именно это и есть рост энтропии.
Вспомните разбитую чашку из первого раздела: переход «целая чашка → осколки» — типичный необратимый процесс. Обратный сценарий физически не запрещён, но настолько статистически невероятен, что в реальности мы его не наблюдаем. Вот такие необратимые процессы задают «стрелу времени».
При этом на уровне отдельных частиц и атомов — законы физики во многом симметричны во времени: фундаментальные уравнения одинаково работают «вперёд» и «назад», и, в принципе, процессы могли бы идти в обе стороны. Но на макроуровне, когда речь идёт о триллионах частиц, появляется статистическая асимметрия: система почти неизбежно переходит в состояния, которым соответствует огромное количество микроконфигураций, — то есть в более вероятные состояния с большей энтропией. Поэтому в среднем энтропия растёт — и это создаёт наблюдаемое нами направление времени от прошлого к будущему.
Но что будет, если применить второе начало термодинамики ко всей Вселенной? Одна из гипотез о её далёком будущем — тепловая смерть. В таком состоянии энтропия достигает максимума, а энергия распределяется почти равномерно: все звёзды погаснут, чёрные дыры испарятся, и останется лишь крайне разреженное, почти однородное излучение и материя. В таком пространстве практически не останется перепадов энергии, а значит — и процессов, которые эти перепады «питают». Это и будет состояние, близкое к максимальной энтропии.
Однако это лишь одна из теоретических моделей. Наша Вселенная может продолжать бесконечно расширяться, коллапсировать обратно в сингулярность или перейти в иное состояние, которое мы пока не можем предсказать. Но сама идея тепловой смерти показывает, к какому пределу ведёт второе начало термодинамики, если применить его к Вселенной как изолированной системе.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!