Что такое среднеквадратичное отклонение и как его рассчитать
Разбираемся на примере нестабильного Wi‑Fi.

Компания перевела четырёх айтишников на удалёнку и каждому выдала по Wi‑Fi-роутеру разных провайдеров. Чтобы понять, какой провайдер лучше, сотрудников попросили в течение дня несколько раз замерять скорость интернета. И вот какие результаты они получили:
- Первый: 96, 98, 102, 100, 100, 104, 98.
- Второй: 140, 20, 170, 50, 130, 160, 30.
- Третий: 110, 108, 104, 94, 106, 112, 90.
- Четвёртый: 20, 20, 180, 180, 20, 140, 120.
Несмотря на примерно одинаковую среднюю скорость — около 100 Мбит/с, — качество интернета у всех было разным. Кто-то мог спокойно работать, у других периодически возникали задержки, а кому-то постоянно приходилось перезагружать роутер, чтобы восстановить соединение.
Чтобы понять причину таких различий, недостаточно посмотреть на среднюю скорость. Важно определить, насколько сильно скорость интернета колеблется в течение дня. Для этого есть специальный показатель — среднеквадратичное отклонение (СКО). Давайте разберёмся, что такое СКО и как его рассчитать — вручную или с помощью Python.
Содержание
- Что такое среднеквадратичное отклонение в статистике
- Как вычислить среднее квадратическое отклонение по формуле
- Как посчитать среднеквадратическое отклонение с помощью Python
Что такое среднеквадратичное отклонение в статистике
Среднеквадратичное отклонение показывает, насколько сильно отдельные значения отличаются от среднего. Чем больше отклонение, тем сильнее разброс данных и меньше предсказуемость. В статистике этот показатель также называют стандартным отклонением, среднеквадратическим отклонением или просто сигмой (σ).
В нашем примере с Wi‑Fi расчёт среднеквадратичного отклонения поможет понять, насколько стабильна скорость интернета у каждого сотрудника. Если СКО будет составлять всего 2–3 Мбит/с — значит, интернет работает стабильно. А вот значение 60–70 Мбит/с укажет на то, что скорость резко скачет и пользоваться таким соединением неудобно.
Прежде чем перейти к расчётам, важно сказать, что среднеквадратичное отклонение связано с другой статистической величиной — дисперсией. Только если дисперсия показывает среднее значение квадратов отклонений от среднего, то среднеквадратичное отклонение — это квадратный корень из дисперсии. В виде формулы это записывается так:
В случае с Wi‑Fi-соединением дисперсия покажет нужный нам разброс значений скорости, однако будет измеряться в неудобных квадратных единицах — (Мбит/с)². Поэтому, чтобы получить результат в привычных единицах (Мбит/с), нам достаточно извлечь квадратный корень из дисперсии. Например, если дисперсия равна 400 (Мбит/с)², то среднеквадратичное отклонение составит 400 = 20 Мбит/с.
При этом без расчёта дисперсии не обойтись. Дело в том, что обычное сложение отклонений от среднего приведёт к тому, что положительные и отрицательные значения взаимно погасят друг друга. Так, если скорости равны 90, 100 и 110 Мбит/с, то их среднее — 100, а отклонения — −10, 0 и 10. В сумме получится ноль, хотя разброс здесь явно есть. А вот если все отклонения сначала возвести в квадрат, то можно избавиться от отрицательных значений и учесть реальную величину разброса.

Читайте также:
Как вычислить среднее квадратическое отклонение вручную по формуле
Начнём с формулы, которая поможет нам вычислить дисперсию:
Расшифруем элементы формулы:
- xᵢ — каждое отдельное значение в наборе данных.
- x̄ — среднее арифметическое всех значений.
- xᵢ − x̄ — отклонение каждого значения от среднего.
- (xᵢ − x̄)² — квадрат отклонения.
- ∑ — сумма всех квадратов отклонений.
- n — общее количество значений в наборе данных.
Дальше мы разберём, как рассчитать дисперсию для первого сотрудника. Затем извлечём квадратный корень, получим среднеквадратичное отклонение и сделаем выводы о стабильности интернет-соединения.
Шаг 1. Сложим все измерения, разделим полученную сумму на их количество и найдём среднюю скорость интернет-соединения:
x̄ = (96 + 98 + 102 + 100 + 100 + 104 + 98) / 7 ≈ 99,71 Мбит/с.
Шаг 2. Вычтем из каждого значения среднее арифметическое, чтобы получить отклонение каждого измерения от среднего (xᵢ − x̄):
- 96 − 99,71 = −3,71.
- 98 − 99,71 = −1,71.
- 102 − 99,71 = 2,29.
- 100 − 99,71 = 0,29.
- 100 − 99,71 = 0,29.
- 104 − 99,71 = 4,29.
- 98 − 99,71 = −1,71.
Шаг 3. Возведём все отклонения в квадрат и избавимся от знаков минуса:
- (−3,71)² = 13,76.
- (−1,71)² = 2,92.
- (2,29)² = 5,24.
- (0,29)² = 0,08.
- (0,29)² = 0,08.
- (4,29)² = 18,40.
- (−1,71)² = 2,92.
И теперь давайте сразу сложим все квадраты отклонений:
13,76 + 2,92 + 5,24 + 0,08 + 0,08 + 18,40 + 2,92 = 43,4 (Мбит/с)².
Шаг 4. Нам осталось разделить сумму квадратов отклонений на количество значений, чтобы узнать дисперсию: 43,4 / 7 = 6,2 (Мбит/с)².
Шаг 5. Извлекаем квадратный корень из дисперсии и, наконец, получаем среднеквадратичное отклонение: 6,2 ≈ 2,49 Мбит/с. Такое небольшое значение СКО указывает на то, что соединение у первого айтишника было довольно стабильным и он, скорее всего, работал без каких-либо сбоев.
Мы рассчитали среднеквадратичное отклонение только для первого сотрудника, но нужно проанализировать ещё трёх. Чтобы не повторять все шаги вручную, можно воспользоваться онлайн-калькуляторами или написать собственную программу. Первый вариант удобен для разовых расчётов, а второй подойдёт, если вы хотите выполнять такие вычисления регулярно и гибко настраивать процесс под себя. Давайте выберем второй способ и в следующем разделе напишем программу для расчёта СКО,
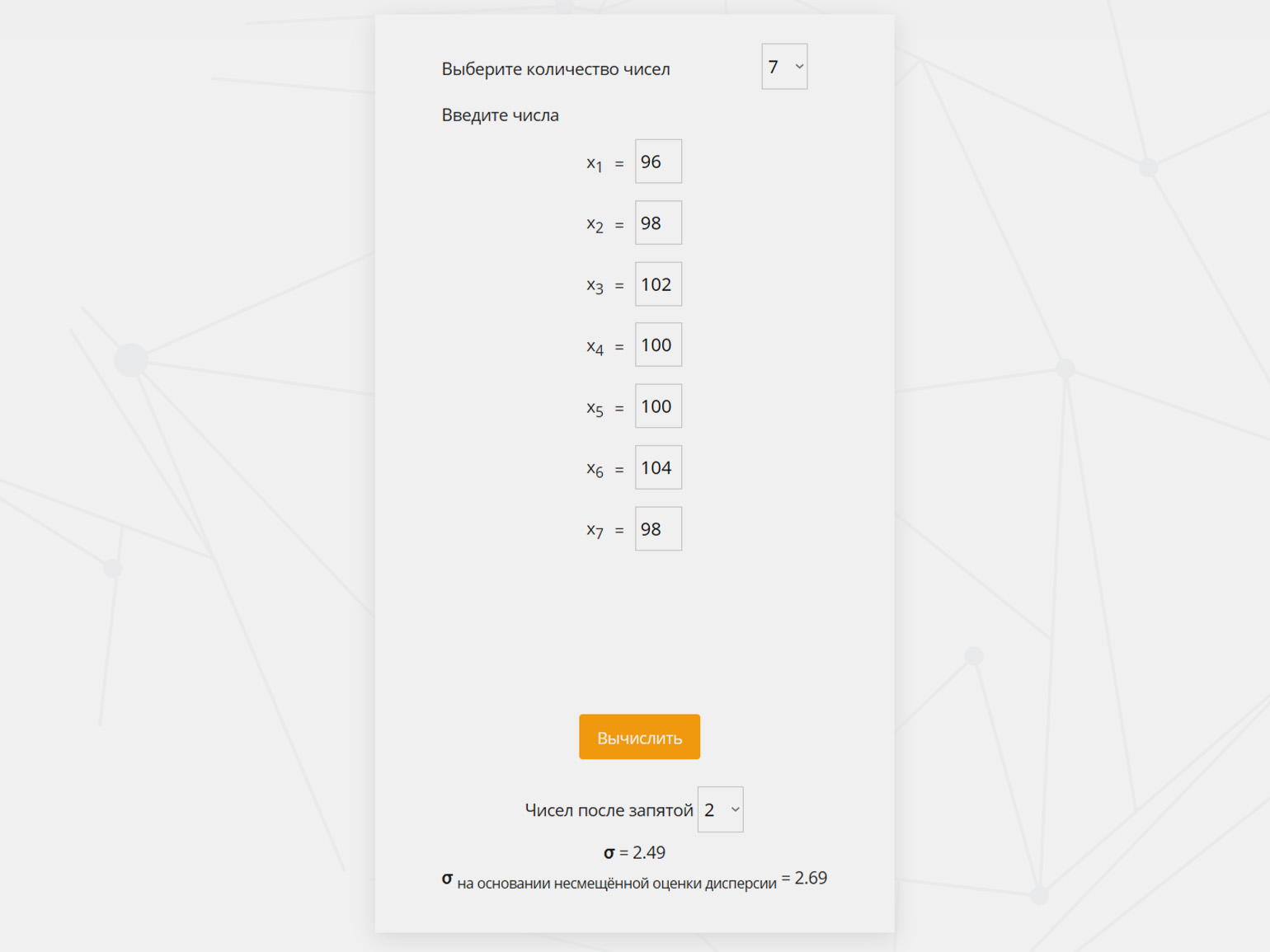
Однако у сервиса есть ограничения: он принимает только от 2 до 30 чисел. Если вам нужно рассчитать СКО для 31 значения, то придётся искать другой инструмент. Кроме того, этот калькулятор не позволяет настраивать параметры — например, посчитать взвешенную дисперсию. Поэтому иногда удобнее написать собственный калькулятор
Изображение: AllCalc / Skillbox Media
Как посчитать среднеквадратическое отклонение с помощью Python
Мы не будем устанавливать Python на компьютер и настраивать редактор кода. Вместо этого перейдите на сайт бесплатного сервиса Google Colab, создайте новый блокнот и вставьте следующий код в пустую ячейку:
import math
# Запрашиваем данные
data = input("Введите значения через пробел или запятую: ")
# Преобразуем введённую строку в список чисел
try:
# Заменяем запятые на пробелы и разбиваем строку на отдельные элементы
numbers = list(map(float, data.replace(',', ' ').split()))
except ValueError:
# Если не удалось преобразовать хотя бы одно значение в число — выводим сообщение об ошибке
print("Ошибка: введите только числа, разделённые пробелами или запятыми.")
numbers = []
# Проверяем, что список не пустой
if numbers:
n = len(numbers) # Количество элементов
mean = sum(numbers) / n # Среднее арифметическое
# Вычисляем квадраты отклонений от среднего для каждого значения
squared_diffs = [(x - mean) ** 2 for x in numbers]
variance = sum(squared_diffs) / n # Дисперсия
std_deviation = math.sqrt(variance) # Среднеквадратичное отклонение
# Выводим результаты
print(f"Среднее значение: {mean:.2f}")
print(f"Дисперсия: {variance:.2f}")
print(f"Среднеквадратичное отклонение: {std_deviation:.2f}")
else:
print("Расчёт не выполнен.")Теперь вы можете ввести любой набор чисел и сразу получить все нужные показатели. Например, если ввести значения для второго сотрудника, программа покажет среднее значение (100), дисперсию (3542,86) и среднеквадратичное отклонение (59,52). При этом вы всегда можете изменить формулу или настроить вывод под свои задачи:
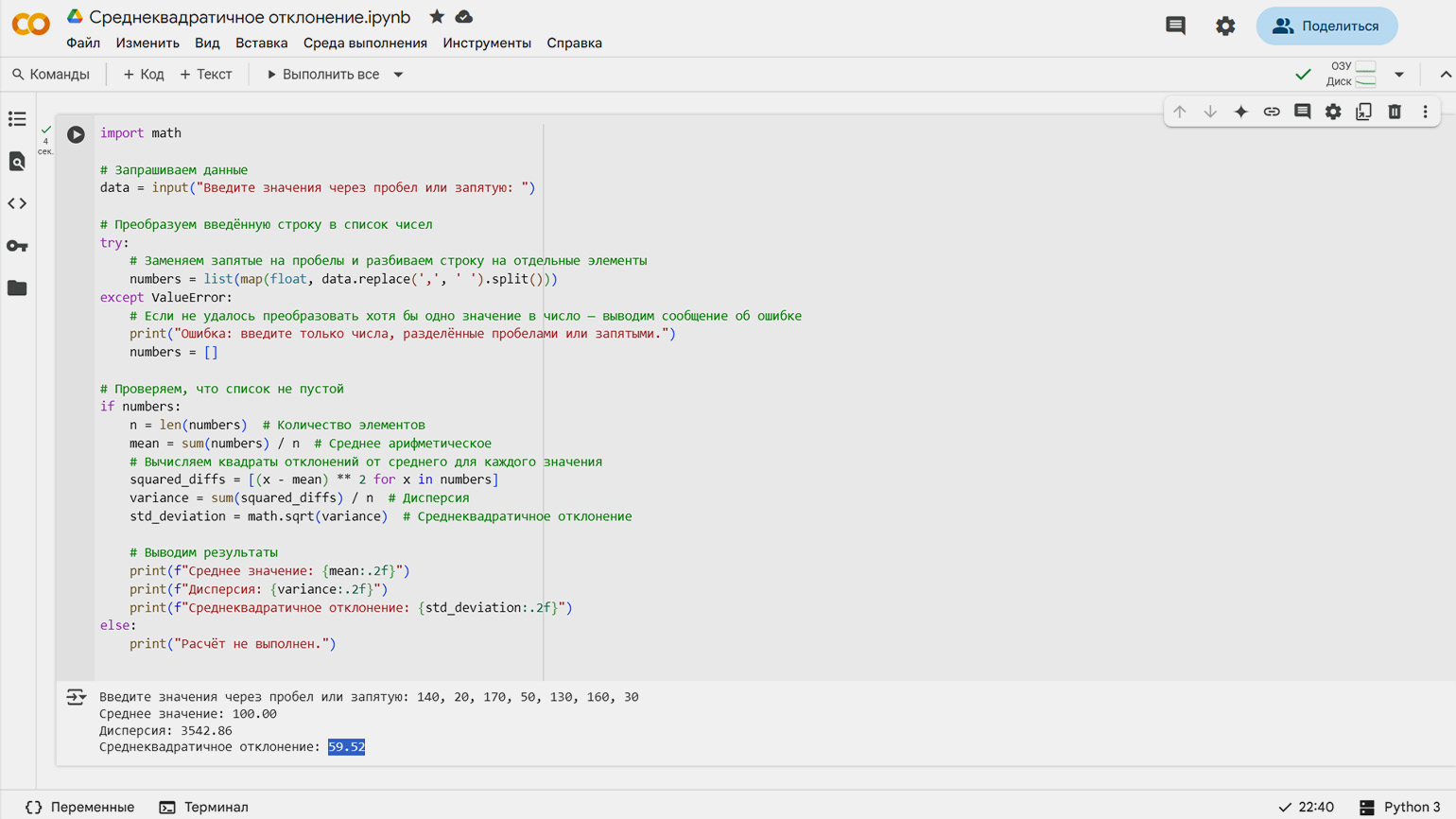
Скриншот: Google Colab / Skillbox Media
С помощью Google Colab мы рассчитали среднеквадратичное отклонение для оставшихся айтишников и теперь можем сравнить результаты:
- 2,49 — у первого почти нет колебаний, соединение надёжное.
- 59,52 — у второго сильные скачки, интернет нестабилен.
- 7,69 — у третьего были небольшие колебания, но в целом соединение стабильное.
- 69,63 — у четвёртого наблюдались самые резкие перепады.
Компании, получившей эти данные, стоит отдать предпочтение первому или третьему провайдеру. Это поможет избежать проблем с обрывами соединения и сэкономить нервы как сотрудникам, так и техподдержке.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!










