Чётные и нечётные функции: что это, чем отличаются и зачем нужны
Предугадываем, куда кривая заведёт.
Графики некоторых функций можно достраивать в любую сторону от нуля оси X безо всяких вычислений. Такие функции называются чётными и нечётными, а их свойства помогают упрощать анализ и расчёты. Рассказываем, как распознать такие функции и какими особенностями они обладают.
Содержание
- Что такое чётные и нечётные функции
- Свойства и признаки чётных и нечётных функций
- Выводы из чётности функции
- Где нужна чётность функции
Что такое чётные и нечётные функции
Чётными функциями называют такие функции, графики которых симметричны относительно оси Y. Это значит, что если отразить график влево или вправо от вертикальной оси, то он не изменится. Математически это записывается как f(−x) = f(x) для всех значений (x) из области определения.
Например, возьмём функцию f(x)= x2.
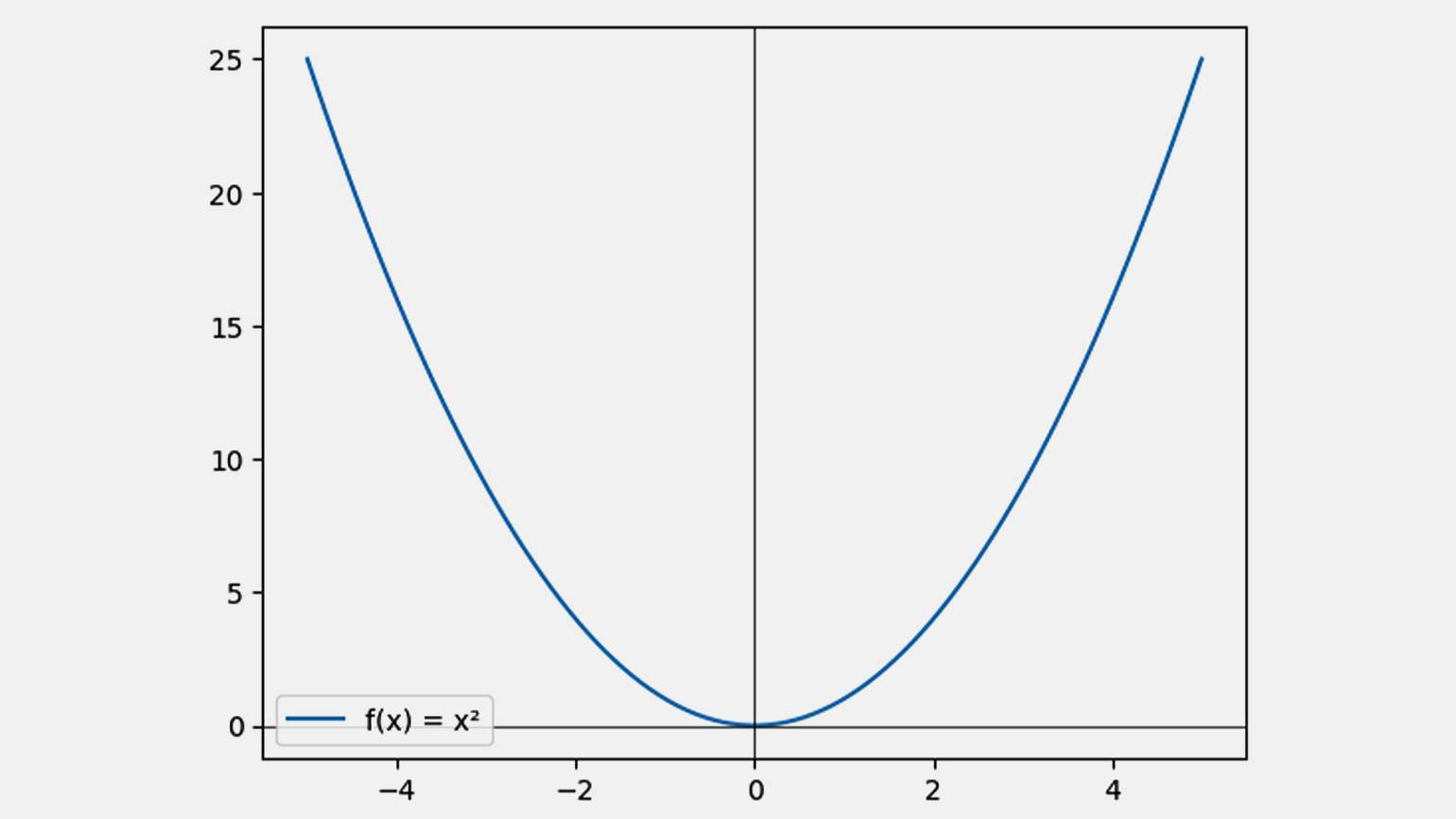
Изображение: Google Colab / Skillbox Media
Если подставить −x, условие выполняется:
Ещё один пример — f(x) = cos(x).
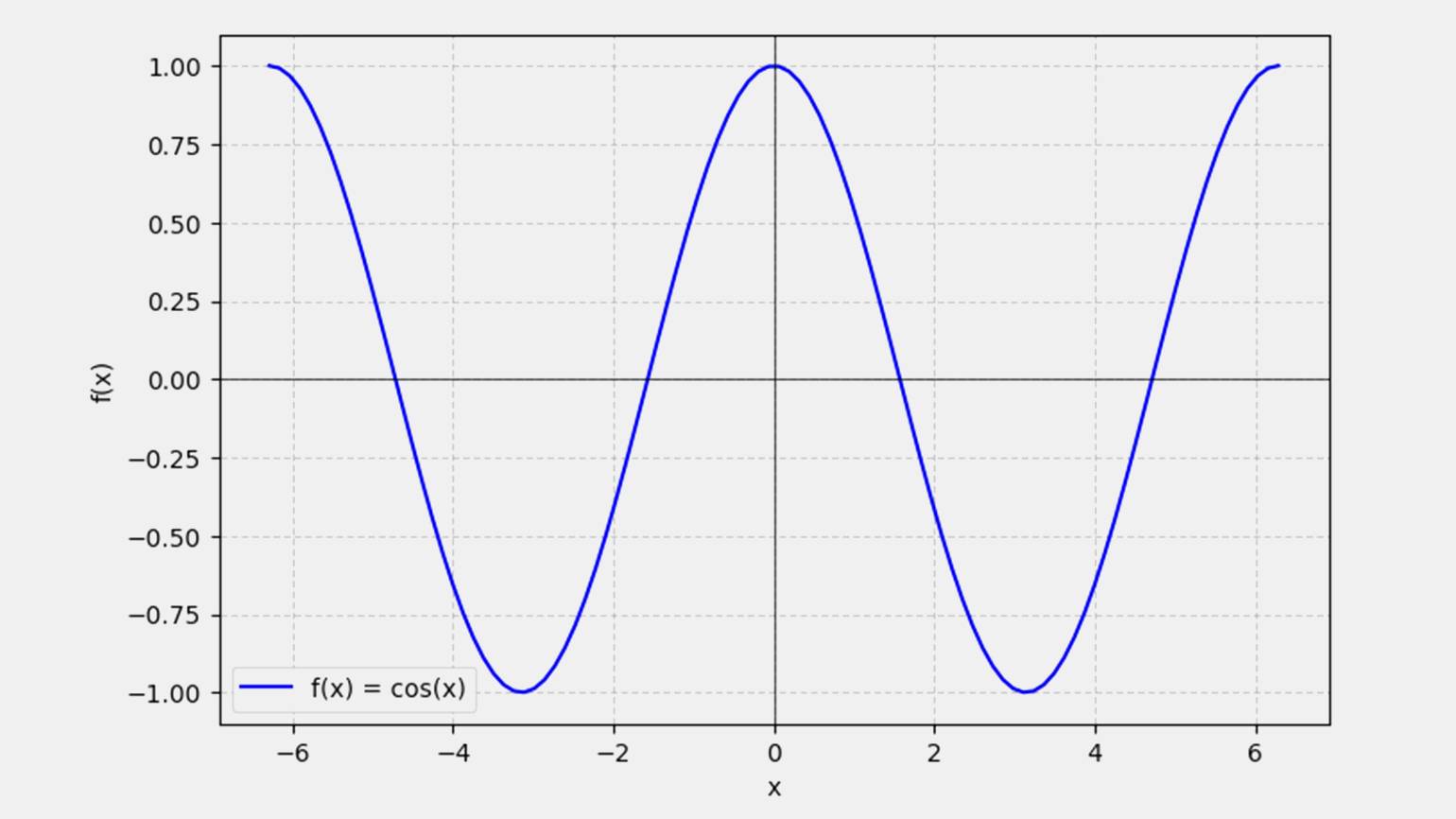
Изображение: Google Colab / Skillbox Media
Косинус тоже не меняется при замене x на −x, ведь cos(−x) = cos (x). Такие функции удобно изучать, потому что их поведение предсказуемо.
Нечётными функциями называют функции, графики которых симметричны относительно начала координат — точки (0,0). Если повернуть график на 180° вокруг этой точки, он останется таким же. В математической форме это f(−x) = −f(x). Например, для f(x) = x3:
Всё сходится.
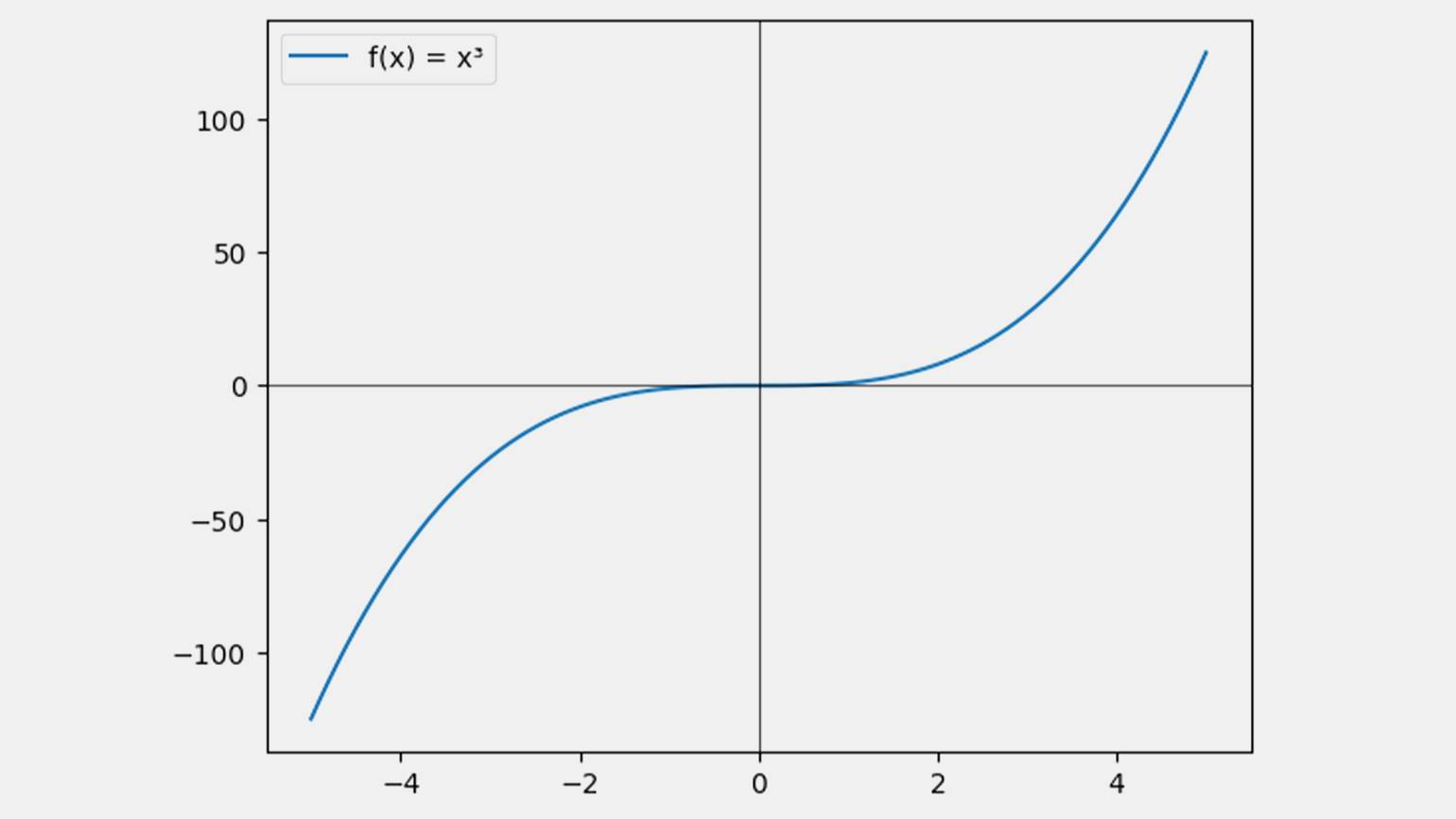
Изображение: Google Colab / Skillbox Media
Другой пример — f(x) = sin(x).
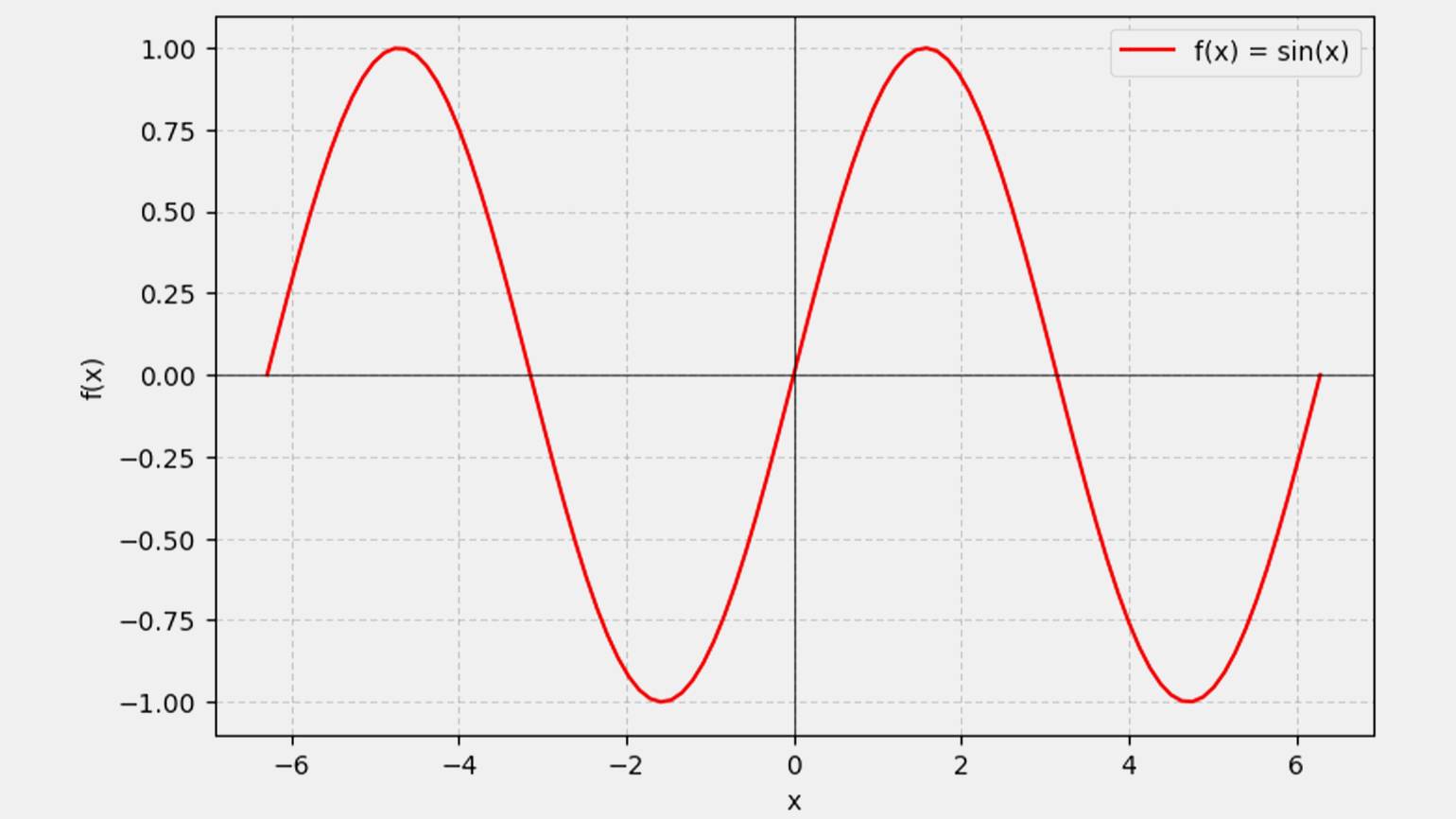
Изображение: Google Colab / Skillbox Media
Это тоже подтверждает нечётность. Такая симметрия означает, что значения функции в положительной и отрицательной областях связаны через противоположный знак.
Функции общего вида — это те, которым несвойственна чётность или нечётность. Их графики не симметричны ни относительно оси y, ни относительно начала координат. Возьмём f(x) = x + 1.

Изображение: Google Colab / Skillbox Media
f(x) = x + 1
f(−x) = −x + 1
−f(x) = −(x +1) = −x − 1
Ни одно из условий не выполняется. Большинство функций в реальной жизни именно такие — без особой симметрии.

Читайте также:
Исключение. Единственная одновременно чётная и нечётная функция —
это f(x) = 0.
Изображение: Google Colab / Skillbox Media
Она удовлетворяет обоим условиям:
f(−x) = 0 = f(x)
f(−x) = 0 = −f(x)
Это уникальный случай, где симметрия относительно оси Y и начала координат сливается в одну прямую линию вдоль оси X.
Свойства и признаки чётных и нечётных функций
Чётные и нечётные функции обладают уникальными свойствами, которые проявляются при математических операциях — от сложения до интегрирования. Эти особенности делают их удобными инструментами для упрощения вычислений и анализа.
Сложение
Сумма двух чётных функций — всегда чётная. Пример: f(x) = x², g (x) = cos (x). Тогда (f + g) (x) = x² + cos (x), и (f + g) (−x) = x² + cos (x) = (f + g) (x).
Сумма двух нечётных функций — нечётная. Пример: f(x) = x³, g (x) = sin (x). Тогда (f + g) (−x) = −x³ − sin (x) = −(f + g) (x).
Сумма чётной и нечётной функций — функция общего вида, не обладающая ни чётностью, ни нечётностью.
Вычитание
Разность двух чётных функций — чётная.
Пример: x² − cos (x) остаётся чётной, так как f(−x) − g (−x) = x² − cos (x).
Разность двух нечётных функций — нечётная.
Пример: x³ − sin (x) при −x даёт −x³ − sin (−x) = −(x³ − sin (x)).
Разность чётной и нечётной функций — функция общего вида.
Умножение
Произведение двух чётных функций — чётное.
Для f(x) = x2 и g (x) = cos (x) получаем:
x2 × cos (x)
f(−x) × g (−x) = (−x)2 × cos (−x) = x2 × cos (x)
Произведение двух нечётных — тоже чётное:
f(x) = x, g (x) = sin (x), x × sin (x), при −x: (−x) × sin (−x) = (−x) × (−sin (x)) = x × sin (x)
А вот чётная на нечётную даёт нечётную:
x2 × x = x3, f(−x) = (−x)3 = −x3 = −f(x).
Деление
Деление двух чётных функций — чётное, если делитель не ноль:
Деление двух нечётных — тоже чётное:
при −x даёт
где sin(x) ≠ 0
А деление чётной на нечётную — нечётное:
При делении главное — следить, чтобы знаменатель не обращался в ноль.
Производная
Производная — это скорость изменения функции. Для чётной функции она всегда нечётная:
если f(x) = x2, то производная f'(x) = 2x, и f'(−x) = 2(−x) = −2x = −f'(x)
У нечётной функции производная чётная:
для f(x) = x3, f'(x) = 3x2, и f'(−x) = 3(−x)2 = 3x2 = f'(x)
Это свойство помогает предсказывать поведение графиков.
Композиция
Композиция — это математическая операция, при которой одна функция применяется к результату другой.
Две чётные дают чётную:
f(x) = x2, g(x) = cos(x), f(g (x)) = cos2(x)
f(g (−x)) = cos2(−x) = cos2(x)
Две нечётные — нечётную:
При f(x) = x3 и g (x) = sin (x)
f(g (x)) = sin3(x), f(g (−x)) = sin3(−x) = −sin3(x).
Чётная и нечётная зависят от порядка:
x2(sin (x)) — чётная
sin(x2) — нечётная
Интеграл
Интеграл — это площадь поверхности под графиком. Для чётной функции на симметричном интервале [−a, a], можно считать только половину:
Например, для x2 от −1 до 1:
Для нечётной функции интеграл на [−a, a] равен нулю:
Так происходит, потому что положительная и отрицательная части отменяют друг друга.
Выводы из чётности функции
Если знать, что функция чётная или нечётная, можно понять её поведение и упростить вычисления. Симметрия подсказывает, как будет выглядеть график, и позволяет сократить работу с формулами.
Чётная функция имеет график, зеркально симметричный относительно оси Y. Это значит, что достаточно рассмотреть её на отрезке от 0 до +∞, а значения для отрицательных x можно восстановить симметрично. Например, для функции
f(x) = x² значения при x = 2 и x = −2 совпадают. Такая симметрия экономит время и при вычислении интегралов:
Нечётная функция симметрична относительно начала координат, и её значения на противоположных сторонах оси X противоположны по знаку. Это приводит к интересному эффекту при интегрировании: на симметричном интервале [-a, a] интеграл равен нулю:
Дело в том что площадь слева от нуля (-0,5) компенсирует площадь справа (+0,5). Это удобно для быстрого анализа.
Функции без симметрии, например f(x) = x + 1, не дают таких упрощений, как чётные и нечётные функции. Их график не зеркален и не поворачивается, поэтому приходится вычислять все значения вручную. Например, интеграл
не упрощается через симметрию — нужно считать полностью.
Где нужна чётность функции
Чётность функций широко используется в науке и технике. Она помогает описывать явления, упрощать расчёты и понимать симметрию в реальном мире. Вот несколько примеров.
Физика. В квантовой механике движение частицы описывается волновой функцией — формулой, которая показывает, где и с какой вероятностью можно найти частицу.
Если функция чётная, то вероятность обнаружить частицу слева и справа от центра одинаковая. Если нечётная — в одних областях вероятность положительная, а в симметричных областях — такая же по величине, но со знаком минус.
То, будет ли функция чётной или нечётной, связано с энергией частицы: разные уровни энергии соответствуют разным видам симметрии.
В квантовой механике волновые функции частиц — это вероятность, с которой частицу можно можно найти в определённом месте — бывают чётными или нечётными. Например, есть часто встречающаяся задача о частице в потенциальной яме — это место в пространстве, где энергия частицы меньше, чем снаружи, поэтому частице «выгодно» там находиться.
Волновые функции — это (x) = cos (kx) (чётная) или (x) = sin (kx) (нечётная). Чётность влияет на вероятность нахождения частицы в разных областях пространства.
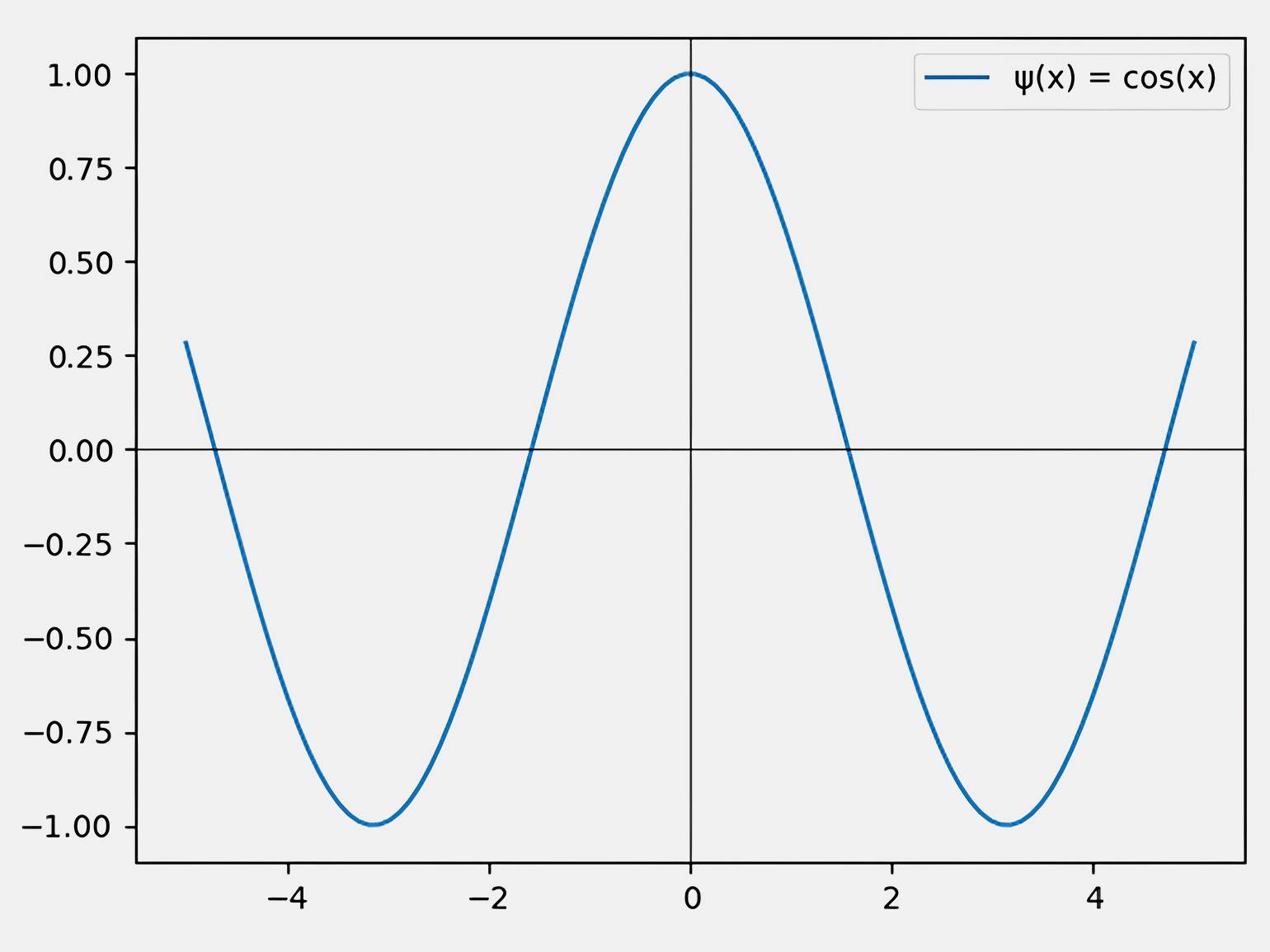
Изображение: Google Colab / Skillbox Media
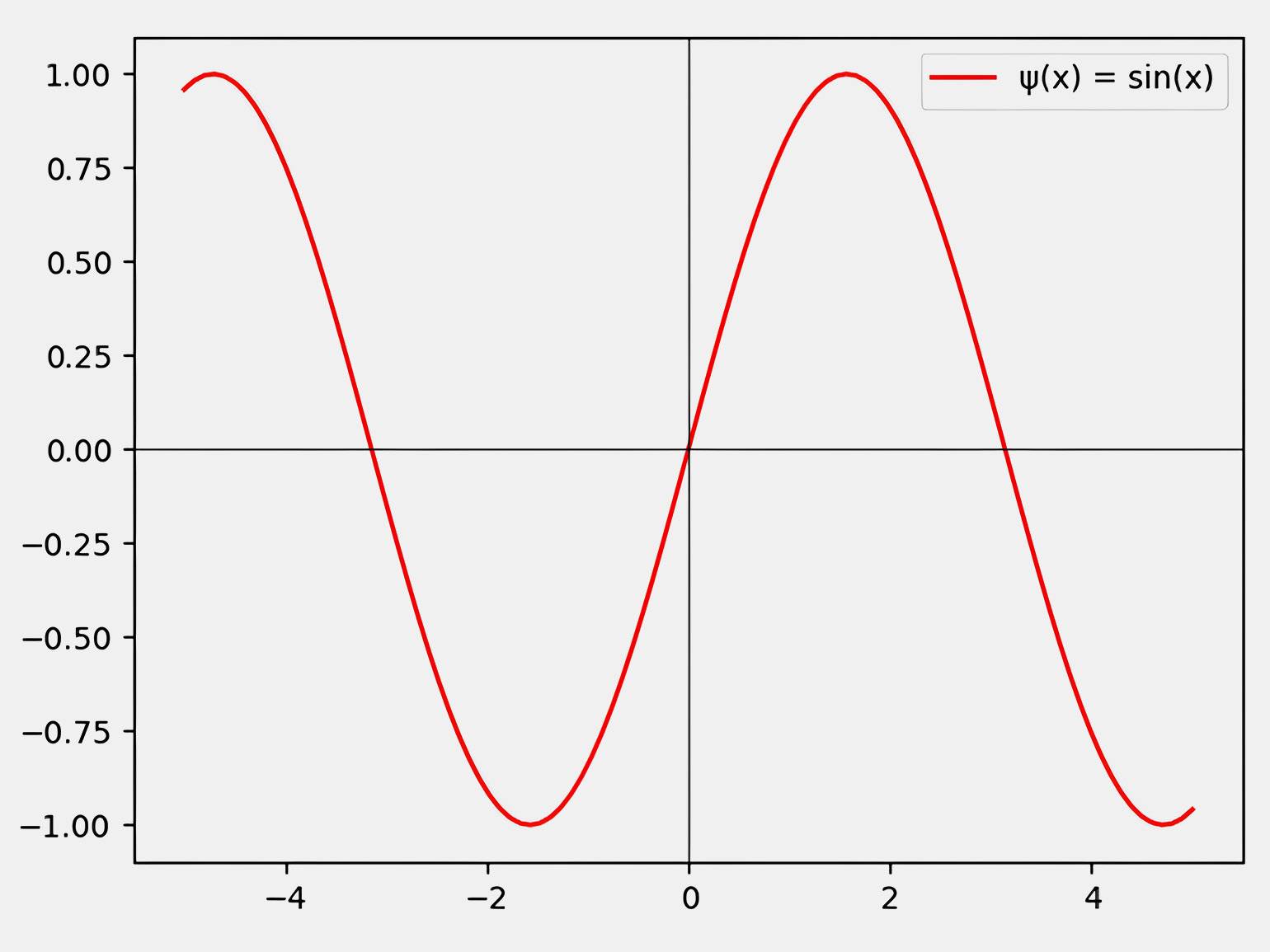
Изображение: Google Colab / Skillbox Media
Математика. В интегральном исчислении чётность ускоряет вычисления. Для чётной функции f(x) = x4 интеграл от −1 до 1:
А для нечётной, вроде x3, он просто ноль на симметричном интервале. Это позволяет быстро решать задачи без лишних расчётов:
Инженерия. В теории сигналов любую функцию можно разложить на две части — чётную и нечётную. Это удобно, потому что такие части связаны с разными базовыми колебаниями:
- чётные компоненты соответствуют косинусам;
- нечётные компоненты соответствуют синусам.
Разложение помогает выделять частотные составляющие сигнала и работать с ними отдельно. В инженерии такие приёмы применяют при проектировании фильтров и систем связи. В смартфоне фильтры обрабатывают Wi-Fi-сигнал: усиливают полезные частоты и убирают лишний шум от соседних сетей.
Например, сигнал s(t) = t + t2 можно разложить на:
Это помогает, например в проектировании систем связи.
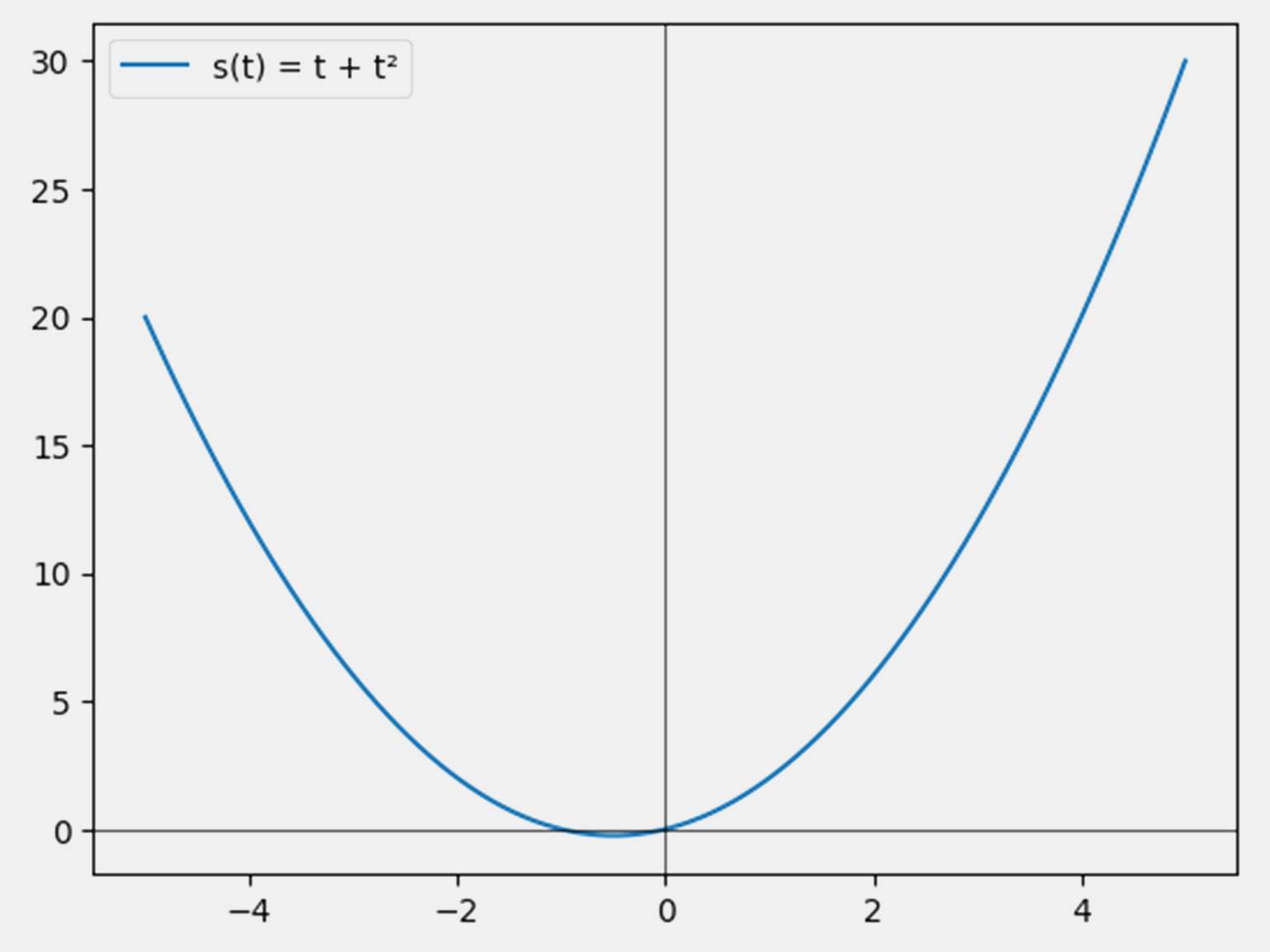
Изображение: Google Colab / Skillbox Media
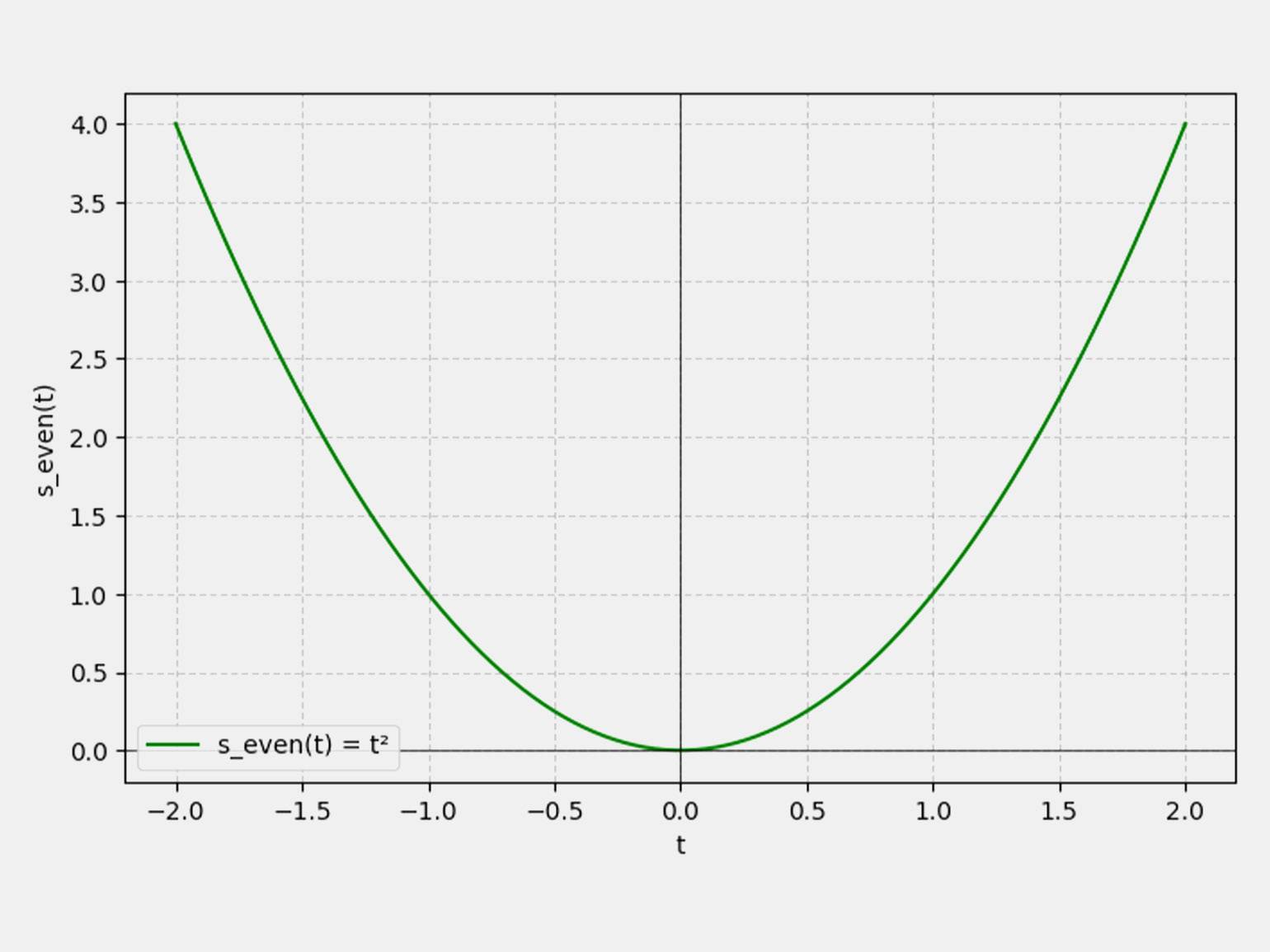
Изображение: Google Colab / Skillbox Media
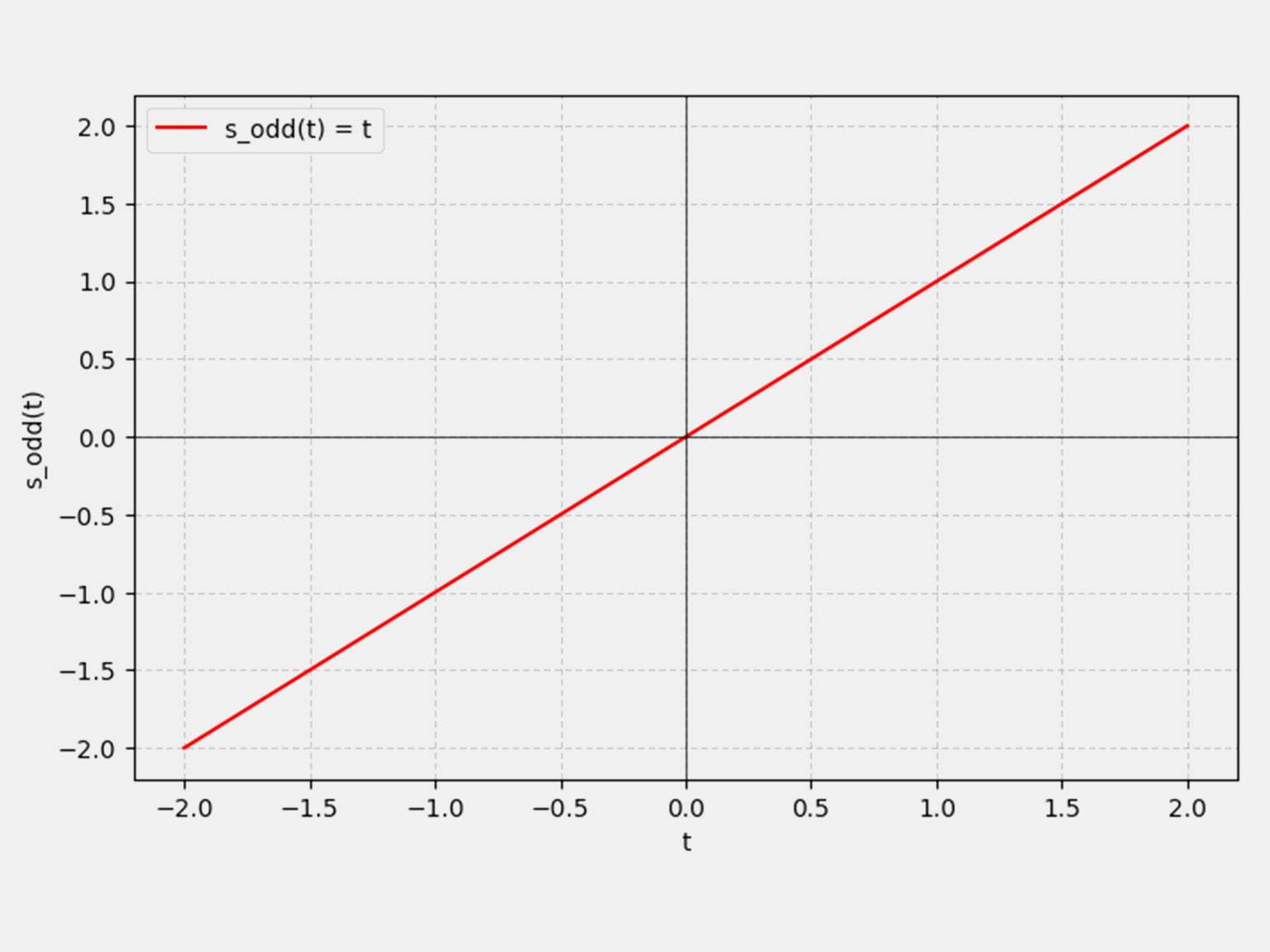
Изображение: Google Colab / Skillbox Media
Что запомнить
Чётные функции симметричны относительно оси Y. Они удовлетворяют условию f(−x) = f(x). Примеры — x2 или cos (x). Эта симметрия упрощает анализ, особенно когда нужно достроить график или посчитать интеграл.
Нечётные функции симметричны относительно начала координат, и для них
f(−x) = −f x). Типичные представители — x3 и sin (x). С ними легко работать: на симметричных интервалах интегралы нечётных функций равны нулю.
У функций общего вида нет никакой симметрии, и с ними приходится работать по полной программе. Например, x + 1 не подчиняется ни одному из правил чётности или нечётности. Это самый распространённый тип функций, и для них нет быстрых математических трюков.
Больше интересного про код — в нашем телеграм-канале. Подписывайтесь!